Bestäm f'''(0) då f(x)=sinx*cosx*exp(x) genom att använda Maclaurinutvecklingar
Frågan lyder:

Och den korrekta lösningen ser ut såhär:
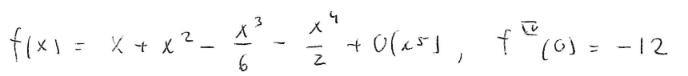
Jag antar att de kört Maclaurinutvecklingar på alla sinx,cosx och exp(x) var för sig sen gångrat ihop de varpå de fick f(x) som står ovan... Vad jag inte förstår är hur f'''(0) blir -12 enligt deras f(x)
Om jag deriverar deras f(x) får jag dessutom -1 då x=0 så jag förstår inte vart de har fått -12 ifrån
De verkar ha kollat på 4e istället. Kan facit vara fel?
Micimacko skrev:De verkar ha kollat på 4e istället. Kan facit vara fel?
Hmmm kanske, men det är lösningsförslaget till en tenta så det känns som det borde stämma.
Hur går man tillväga allmänt? Har hittat en formel som lyder:
f(k)=k!ak
som för fjärdederivatan då ger:
Tänker jag rätt här?
Enligt samma resonemang borde tredjederivatan bli:
Är det inte enklare att bara derivera polynomet än att komma ihåg en formel till?
Men dina svar är rätt.
Micimacko skrev:Är det inte enklare att bara derivera polynomet än att komma ihåg en formel till?
Men dina svar är rätt.
Jo kanske men det är ju en rätt lätt formel att komma ihåg, bara (deriveringsgraden)! gånger koefficienten framför termen av den graden.
Men då får jag anta att facit är fel
Tack för hjälpen!
Micimacko skrev:Är det inte enklare att bara derivera polynomet än att komma ihåg en formel till?
Men dina svar är rätt.
Alltså, det används ju i själva definitionen av maclaurin/taylor-utvecklingar, så om man vet hur man utför en sådan utveckling blir det ingen extra formel att komma ihåg
Beror på hur man ser det. I formeln står det ju f^n(a)*(x-a)/n!
Jag kan lösa ut det därifrån, men det var inte det ts gjorde.
Nä visst, jag försökte påpeka att den formeln som hittats kommer helt naturligt från hur man gör utvecklingarna, så om man lär sig det har man lärt sig den formeln på köpet


