32 svar

297 visningar

Anonym82 behöver inte mer hjälp

Bestäm exakt ekvationen för linjen L

En triangel begränsas av x-axeln, linjen 10x + 29y − 80 = 0 och linjen L. Denna linje L går genom punkten (-8;0). Triangeln har arean 40 areaenheter.
Bestäm exakt ekvationen för linjen L (utan grafisk lösning).

Jag har sett denna uppgiften på nätet, där de visar hur man gör och jag förstår den. Det jag inte förstår är hur de får
10x + 29y − 80 = 0 att bli till 10x + 20y − 80 = 0 -> y = -0,5x + 4.
29y kan väl inte omvandlas till 20y bara sådär? Kan ni snälla förklara hur man löser denna uppgiften korrekt?

Tack i förhand.

Det låter konstigt, men det kan finnas något steg däremellan som förändrar antalet y. Ta det steg för steg. Börja med att rita upp situationen! Hur bred är triangeln? :)

Det ska vara 20 och inte 29, se nedan:

https://www.pluggakuten.se/trad/bestam-ekvationen-20/

tomast80 skrev:
Det ska vara 20 och inte 29, se nedan:
https://www.pluggakuten.se/trad/bestam-ekvationen-20/

På min uppgift står det 29 (10x + 29y - 80 = 0) och inte 20. Det var så på en annan tjejs uppgift med och vi vet inte varför vissa har 20, om det är för att dom omvandlat 29 till 20 på något sätt när dom räknat ut eller vad det handlar om. Det är just det jag inte fattar.

Smutstvätt skrev:
Det låter konstigt, men det kan finnas något steg däremellan som förändrar antalet y. Ta det steg för steg. Börja med att rita upp situationen! Hur bred är triangeln? :)

Hittills av de jag har förstått så borde linjen 10x + 29y - 80 = 0 skära X axeln vid 8 och linjen L skär vid (-8, 0) vilket gör att triangelns bas är 16. Förstår fortfarande inte riktigt hur jag ska bestämma den exakta ekvationen för linjen
L.

Helt korrekt, snyggt! :) Triangeln ska ha arean 40 ae, och med basen 16 le måste då triangelns höjd vara $\frac{16 \cdot h}{2} = 40 h = 5$

En snabb skiss över situationen:

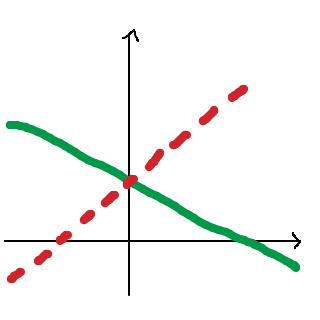
Skärningspunkten mellan den röda (streckade) linjen, som vi söker, och den gröna linjen (som vi har fått) kan vi kalla (a,b). Denna punkt måste uppfylla två krav:

Triangelns höjd blir fem le.
Punkten är en skärningspunkt mellan de två linjerna

Vilken punkt uppfyller dessa krav? :)

Smutstvätt skrev:
Helt korrekt, snyggt! :) Triangeln ska ha arean 40 ae, och med basen 16 le måste då triangelns höjd vara $\frac{16 \cdot h}{2} = 40 h = 5$
En snabb skiss över situationen:
Skärningspunkten mellan den röda (streckade) linjen, som vi söker, och den gröna linjen (som vi har fått) kan vi kalla (a,b). Denna punkt måste uppfylla två krav:
Triangelns höjd blir fem le.
Punkten är en skärningspunkt mellan de två linjerna
Vilken punkt uppfyller dessa krav? :)

Kan denna punkt vara (0, 5)? Eller har jag fel

Punkten kommer absolut ha y-värdet 5 (b = 5). Däremot måste inte x-värdet vara noll (a = 0). Tänk på att punkten ska vara en skärningspunkt, och den måste därför ligga på den gröna linjen. :)

Smutstvätt skrev:
Punkten kommer absolut ha y-värdet 5 (b = 5). Däremot måste inte x-värdet vara noll (a = 0). Tänk på att punkten ska vara en skärningspunkt, och den måste därför ligga på den gröna linjen. :)

Jaha okej kan punkten vara (-2, 5) då?

Nej, punkten $x=-2,y=5$ ligger inte på linjen $10x+29y-80=0$

Testa får du se!

Jroth skrev:
Nej, punkten $x=-2,y=5$ ligger inte på linjen $10x+29y-80=0$
Testa får du se!

Men hur ska jag lista ut detta? Förstår inte hur jag ska ta reda på vilken punkt som ligger på linjen

Du vet att y-värdet ska vara 5. Sätt in det värdet i linjens ekvation, och lös ut x. :)

Smutstvätt skrev:
Du vet att y-värdet ska vara 5. Sätt in det värdet i linjens ekvation, och lös ut x. :)

Jag får fram att x är -6,5 vilket ja inte tror är rätt, vet inte vad jag gör för fel

Det stämmer! Om du är osäker, sätt in x = -6,5 och y = 5 i ekvationen, och se om lösningen stämmer.

Nu har du två punkter på linjen som du söker. :)

Smutstvätt skrev:
Det stämmer! Om du är osäker, sätt in x = -6,5 och y = 5 i ekvationen, och se om lösningen stämmer.
Nu har du två punkter på linjen som du söker. :)

Jaha okej vad bra att det blev rätt, men nu har jag punkten (-6,5 , 5) som är skärningspunkten för båda linjerna och ger triangeln en höjd på 5. Och den andra punkten är då (8,0) antar jag. Men vad gör jag nu med denna information, hur gör jag detta till en ekvation för linjen L? Förlåt är ganska seg i matte så jag kopplar inte så fort.

Jaha okej vad bra att det blev rätt, men nu har jag punkten (-6,5 , 5) som är skärningspunkten för båda linjerna och ger triangeln en höjd på 5. Och den andra punkten är då (8,0) antar jag.

Korrekt!

Men vad gör jag nu med denna information, hur gör jag detta till en ekvation för linjen L?

En rät linje kan skrivas på formen $y=kx+m$ . k kan beräknas som $k=\frac{y_2-y_1}{x_2-x_1}$ . Därefter kan du sätta in en av punkterna i $y=kx+m$ (där k är bestämt), och hitta m. :)

Smutstvätt skrev:
Jaha okej vad bra att det blev rätt, men nu har jag punkten (-6,5 , 5) som är skärningspunkten för båda linjerna och ger triangeln en höjd på 5. Och den andra punkten är då (8,0) antar jag.
Korrekt!
Men vad gör jag nu med denna information, hur gör jag detta till en ekvation för linjen L?
En rät linje kan skrivas på formen $y=kx+m$ . k kan beräknas som $k=\frac{y_2-y_1}{x_2-x_1}$ . Därefter kan du sätta in en av punkterna i $y=kx+m$ (där k är bestämt), och hitta m. :)

Jag räknade nu ut K och M värdet och fick fram att K = -3,0 och M = 3,05. Jag sätter nu in detta i formen - y = - 0,3x + 3,05.
Är detta rätt? Vad gör jag sen?

Anonym82 skrev:
Smutstvätt skrev:
Jaha okej vad bra att det blev rätt, men nu har jag punkten (-6,5 , 5) som är skärningspunkten för båda linjerna och ger triangeln en höjd på 5. Och den andra punkten är då (8,0) antar jag.
Korrekt!
Men vad gör jag nu med denna information, hur gör jag detta till en ekvation för linjen L?
En rät linje kan skrivas på formen $y=kx+m$ . k kan beräknas som $k=\frac{y_2-y_1}{x_2-x_1}$ . Därefter kan du sätta in en av punkterna i $y=kx+m$ (där k är bestämt), och hitta m. :)
Jag räknade nu ut K och M värdet och fick fram att K = -0,3 och M = 3,05. Jag sätter nu in detta i formen - y = - 0,3x + 3,05.
Är detta rätt? Vad gör jag sen?

Är den bestämda ekvationen för linjen L detta: 5 = -0,3*-6,5 + 3,05? Jag la in en av punkterna i formen och samt k och m värdet.

Anonym82 skrev:
Jag räknade nu ut K och M värdet och fick fram att K = -3,0 och M = 3,05. Jag sätter nu in detta i formen - y = - 0,3x + 3,05.
Är detta rätt? Vad gör jag sen?

Nja, det stämmer inte riktigt. Kan du skriva ned dina uträkningar, så kan vi se var det blivit knas? :)

Smutstvätt skrev:
Anonym82 skrev:
Jag räknade nu ut K och M värdet och fick fram att K = -3,0 och M = 3,05. Jag sätter nu in detta i formen - y = - 0,3x + 3,05.
Är detta rätt? Vad gör jag sen?
Nja, det stämmer inte riktigt. Kan du skriva ned dina uträkningar, så kan vi se var det blivit knas? :)

Glömde påpeka att K-värdet ska vara -0,3 och inte -3,0, skrev fel där.. Men här är mina uträkningar:

För att ta reda på K gjorde jag så här: $k \frac{y_{1} - y_{2}}{x_{1} - x_{2}} = \frac{0 - 5}{8 - (- 6, 5)} = \frac{- 5}{14, 5} = - 0, 3$

För att ta reda på m:

5 = -0,3 * -6,5 + m

sedan multiplicerar jag -0,3 och -6,5 vilket blir:

5 = 1,95 + m

Jag subtraherar sedan 1,95 både på höger led och vänsterled.

vilket ger mig 3,05 som jag tänker är M-värdet.

Vart gjorde jag fel :(

Det är helt rätt teknik, men du har missat ett litet minustecken. Vilket värde har $x_1$ ? :)

Smutstvätt skrev:
Det är helt rätt teknik, men du har missat ett litet minustecken. Vilket värde har $x_1$ ? :)

Ojdå, glömde minustecknet framför 8:an.. Vad klumpigt.
Nu fick jag fram att K-värdet är 3,3 istället, stämmer det?

Ja, k-värdet är 3,333... :)

Smutstvätt skrev:
Ja, k-värdet är 3,333... :)

Ska jag skriva K-värdet som 3,333 eller bara 3,3 när jag lägger in det i y=kx+m för att räkna ut m-värdet?

Skriv det i bråkform, dvs. som 10/3, när du beräknar m-värdet. :)

Smutstvätt skrev:
Skriv det i bråkform, dvs. som 10/3, när du beräknar m-värdet. :)

Jag får fram att M är -11,661... Är detta korrekt?

Det låter inte helt korrekt. Du kan alltid sätta in punkterna och prova. Hur har du fått fram ditt m?

Smutstvätt skrev:
Det låter inte helt korrekt. Du kan alltid sätta in punkterna och prova. Hur har du fått fram ditt m?

5 = (10/3)*3500+m

5=11,666+m

Subtraherade 11,666 både på vänsterled och högerled
fick: -11,661

Vänta lite, var kommer 3500 från? Ta punkten (-6,5 ; 5):

$5 = \frac{10}{3} \cdot (- 6, 5) + m 5 = (- 21 + \frac{2}{3}) + m m = 5 + \frac{2}{3} + 21 = 26, 666 . . .$

m är lika med $26 + \frac{2}{3}$ , eller $\frac{80}{3}$ . :)

Smutstvätt skrev:
Vänta lite, var kommer 3500 från? Ta punkten (-6,5 ; 5):
$5 = \frac{10}{3} \cdot (- 6, 5) + m 5 = (- 21 + \frac{2}{3}) + m m = 5 + \frac{2}{3} + 21 = 26, 666 . . .$
m är lika med $26 + \frac{2}{3}$ , eller $\frac{80}{3}$ . :)

Jahaa oj! Råkade använda x-punkten av en annan uppgift jag arbetade med samtidigt och blandade ihop dem.. klumpigt av mig, men nu förstår jag tack!
Det jag nu undrar är hur ja ska sätta all denna information till en bestämd ekvation för Linjen L, jag har en punkten (-6,5, 5) samt k-värdet (10/3) och M värdet (80/3). Hur borde jag göra för att sätta ihop detta till en bestämd ekvation?

Ingen fara, sådant händer!

Räta linjens ekvation ger att ekvationen kan skrivas på formen $y=kx+m$ , så nu behöver du bara sätta in värdena k och m, så har du din ekvation. :)

Smutstvätt skrev:
Ingen fara, sådant händer!
Räta linjens ekvation ger att ekvationen kan skrivas på formen $y=kx+m$ , så nu behöver du bara sätta in värdena k och m, så har du din ekvation. :)

Så det ska se ut så här Y=10/3x+80/3? Behöver jag sätta in någon punkt eller bara så där?

Precis så! Du behöver inte sätta in en punkt, det gör du endast om du vill hitta y-värdet givet ett x-värde, eller tvärtom. :)

Svara

Visa senaste svar