Bestäm exakt det största värdet på rektangelarean
Hej!
Uppgiften lyder: "På kurvan y=4-2x, 0<𝑥<4, väljer man en punkt P. Från P drar man en linje vinkelrät mot x-axeln och en linje vinkelrät mot y-axeln så att en rektangel bildas. Bestäm exakt det största värdet på rektangelarean."
Jag ritade upp det på följande sätt och fick svaret till 2 a.e.

Detta var tydligen fel, förklaringen jag fick av läraren var "Det står att x varieras från 0 till 4, då kan skaffas en triangel i den fjärde kvadraten. Om du flyttar punkt P under x-axel då får du en rektangel till"
Jag förstår inte riktigt hur jag ska få till en rektangel med punkten P under x-axeln. Finns det någon som kan ge en ledtråd möjligtvis?
Mvh Förvirrad
Om du sätter punkten P på linjen där x=4 och drar de vinkelräta linjerna till axlarna, hur ser rektangeln ut då?
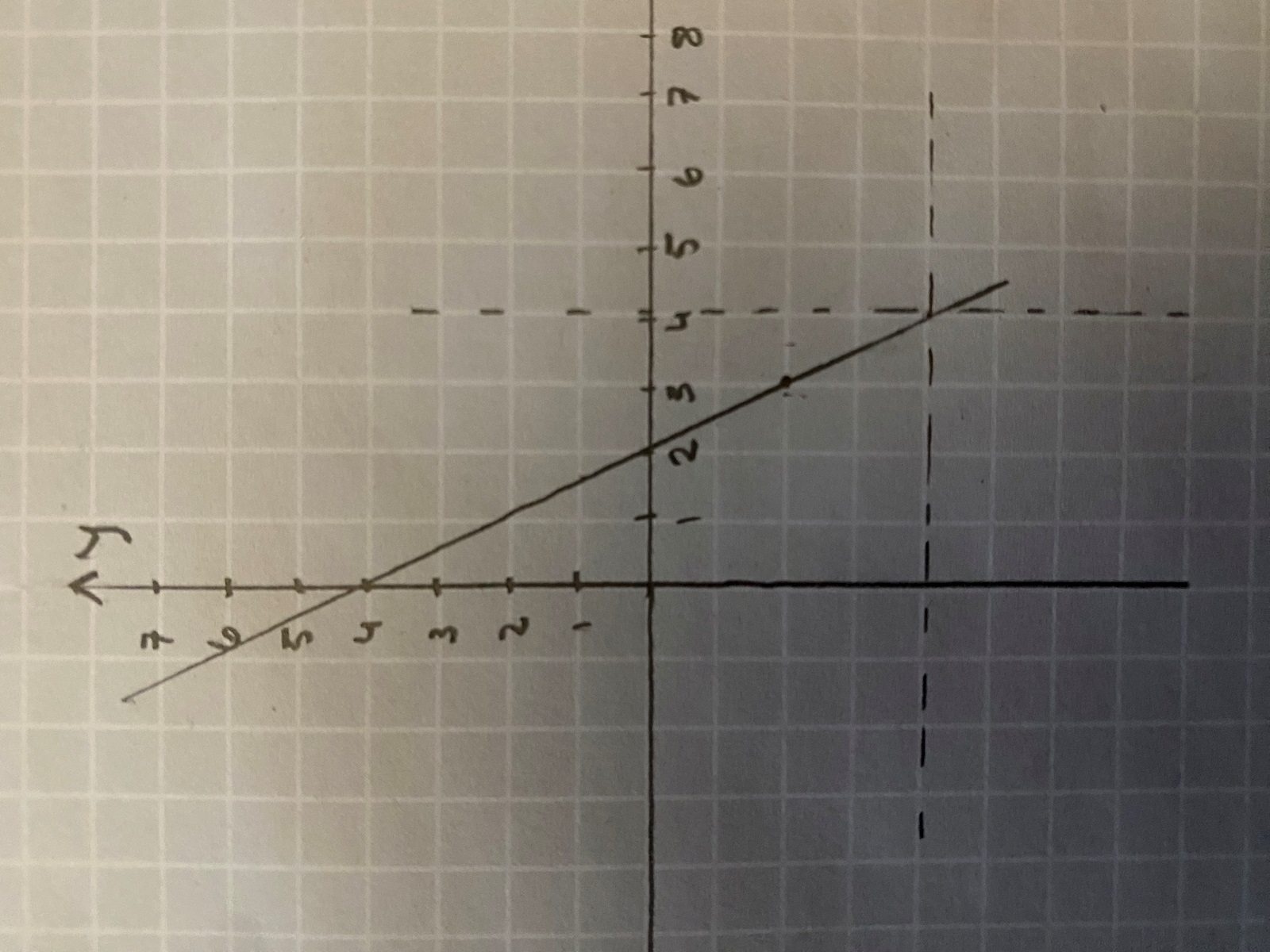
Menar du så? Jag tänkte på det men linjen går rakt igenom.. spelar det någon roll?
(edit: punkten vid x=3 är gammalt)
Ja, så tror jag att man har tänkt sig!
louise.marsch skrev:
Menar du så? Jag tänkte på det men linjen går rakt igenom.. spelar det någon roll?
(edit: punkten vid x=3 är gammalt)
Precis. Det står inget om att linjen inte får gå igenom rektangeln.
Tack för hjälpen! jag fick arean till 8 a.e denna gång. Fått feedback att detta inte stämde då x=3 ger negativ area. Förstod inte riktigt och har inte fått mer svar än. Någon här som kan hjälpa så länge? Känns som att detta egentligen är busenkelt men jag missar något i mina uträkningar :')
Hade du integrerat funktionen y = 4-2x från k till 4, möjligen? Och sedan deriverat arean för att se när arean är som störst. I så fall kan jag förstå kommentaren.
Jag har tyvärr inte kvar uträkningarna så minns inte exakt hur jag gjorde... men jag gjorde om de nu och fick det till -16 a.e, kan det stämma?
Om du väljer att räkna för den undre rektangeln, så är integranden inte f(x) utan 0-f(x). Din lärare har rätt i att en area inte kan vara negativ.
alltså 16 a.e?
Ja, om rektangeln har sitt hörn i punkten (4,-4) så blir arean 16 ae. Men väldigt mycket hänger på hur väl du har redovisat hur du har resonerat.
Det var så jag uppfattade det
Det är mycket som inte stämmer här. Till att börja med behöver du dela upp beräkningarna i två fall, om x < 2 (så att rektangeln ligger ovanför x-axeln) så stämmer det att arean = xy, men om x > 2 så är arean = x(-y). I Ma5 skule jag också förvänta mig att man motiverar VARFÖR detta är den största arean, d v s dels att man undersöker var derivatan är 0, dels att man undersöker alla randpunkter.





