bestäm ett uttryck för sidan (d) i den rätvinkliga triangeln

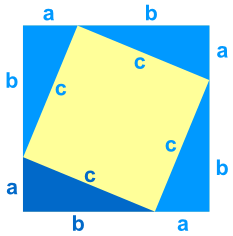
Det finns en matematisk regel (kallas för sats eller teorem) som säger att summan av kateternas kvadrater är lika med kvadraten av hypotenusan. Detta är Pythagoras sats. Det finns många bevis för att satsen är sann. Du kan googla på nätet och hitta bilder som hjälper en (åtminstone mig) att intuitivt förstå vad satsen säger. Se t.ex. bilden nedan

Natascha skrev :

Hej allihopa. 

Jag fick en uppgift idag i skolan och minns att jag klurade en stund på den, jag vill ta upp den här ännu en gång för lite djupare förklaring... 

Vi har en rätvinklig triangel och båda kateterna är betecknade med variabeln (a) och hypotenusan med (d). Jag ska utifrån denna information skriva ett uttryck för hypotenusan. 

Kan någon hjälpa mig hur man kan ta sig an en sådan uppgift...? :)

Använd Pythagoras sats.

Den lyder som följer:

I en rätvinklig triangel med kateter a och b och hypotenusan c så gäller följande samband: $a^2+b^2=c^2$.

Eftersom båda kateterna i ditt fall har längden a och hypotenusan kallas för d så får du följande samband: $a^2+a^2=d^2$.

Din uppgift nu blir att lösa ut d ur detta samband. Behöver du hjälp med det?

Yngve skrev :

Natascha skrev :

Hej allihopa. 

Jag fick en uppgift idag i skolan och minns att jag klurade en stund på den, jag vill ta upp den här ännu en gång för lite djupare förklaring... 

Vi har en rätvinklig triangel och båda kateterna är betecknade med variabeln (a) och hypotenusan med (d). Jag ska utifrån denna information skriva ett uttryck för hypotenusan. 

Kan någon hjälpa mig hur man kan ta sig an en sådan uppgift...? :)

Använd Pythagoras sats.

Den lyder som följer:

I en rätvinklig triangel med kateter a och b och hypotenusan c så gäller följande samband: $a^2+b^2=c^2$.

 

Eftersom båda kateterna i ditt fall har längden a och hypotenusan kallas för d så får du följande samband: $a^2+a^2=d^2$.

Din uppgift nu blir att lösa ut d ur detta samband. Behöver du hjälp med det?

Hej Yngve. 

Jag har skrivit upp den ekvationen också och försöker att reda ut ett "uttryck för d". Jag förstår inte hur jag ska börja efter att jag skrivit "$a^2 + a^2 = d^2$" Jag behöver hjälp!

$$\begin{gathered} a^2 + a^2 = d^2 \\ a*a + a*a = d*d \\ {d}^2(a^{2 } + a^2) \end{gathered}$$Kan man börja såhär... ? 

Hmm vad händer med likhetstecknet?

Nej det där blir lite konstigt. Utan du har ju

$a^2 + a^2 = d^2$

Du har alltså två stycken $a^2$ i VL så man kan skriva om det som

$2a^2 = d^2$

Nu kan du dra roten ur båda sidorna

$\sqrt{2a^2} = \sqrt{d^2}$

Nu använder vi att $\sqrt{2a^2} = \sqrt{2} \cdot \sqrt{a^2} = \sqrt{2}\cdot a$. Samt att $\sqrt{d^2} = d$. Därför får man

$\sqrt{2}\cdot a = d$.

Ahh, jag började skriva Stokastisk så som du gjorde men jag trodde att om jag skriver "a upphöjt till 2 + a upphöjt till 2" och skriver om det som "2a upphöjt till 2" så blir det fel... 

Jag vet inte riktigt vart jag hamnade... 

Tack för hjälpen Stokastisk!