Bestäm ett p(x) av högst graden sådant att funktionen blir deriverbar
Hej!
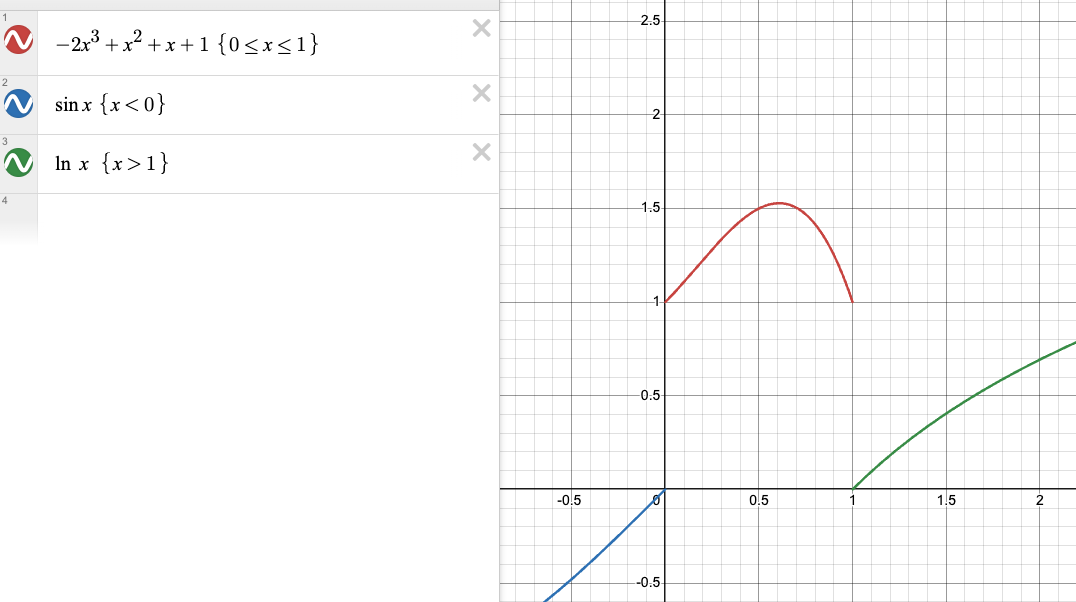
jag fick fram P(x) mha kontinuitet och deriverbarhet. Polynomet blir då -2x^3+x^2+x+1. Men när jag testar att titta på om p(x) är deriverbar i punkten x=1 så får jag dess derivata värde till -3 medan för derivatans värde till ln(x) så blir det bara ett. Jag vet inte om man kan göra så , men för kontinuitet stämmer det i alla fall. Jag tänker om funktionen är deriverbar i [0,1] så är den kontinuerlig också (sats 8.7) , men räcker det som motivering trots att derivatans värde skiljer sig i just punkten x=1

Nej, den blir ej kontinuerlig
teknikomatte skrev:Nej, den blir ej kontinuerlig
Juste D är ju 0. Min funktion är alltså P(x)= -2x^3+x^2+x+0, jag råkade skriva med 1.
Då är den kontinuerlig, men man ser att den inte alls är deriverbar i 0 och 1. Hur räknade du ut polynomet?
Eller i alla fall inte i x = 1.
Laguna skrev:Då är den kontinuerlig, men man ser att den inte alls är deriverbar i 0 och 1. Hur räknade du ut polynomet?
Fast jag fick att den är deriverbar i punkten x=0 men inte i punkten x=1 och nu syftar jag på p(x)=-2x^3+x^2+x+0 och inte den som är p(x) = -2x^3+x^2+x+1. Jo jag gjorde kontinutiet lim x=> 0+ f(x)= lim x=> 0- f(x). sen körde jag derivatan av båda leden och samma sak med punkten x=1. Då fick jag 4 ekvationer och två obekanta.
Vad ska derivatan vara för x = 1?
Laguna skrev:Vad ska derivatan vara för x = 1?
Om vi tittar på när x närmar sig 1 från plus hållet så blir derivatans värde för ln(x)= 1 medan om vi närmar oss 1 från negativa hållet så blir derivatans värde för p'(x)=-3
Mhm, och vad säger uppgiften att du ska göra?
Laguna skrev:Mhm, och vad säger uppgiften att du ska göra?
Ja vi ska bestämma P(x) så att f(x) blir deriverbar.
Är din funktion deriverbar för x = 1?
Laguna skrev:Är din funktion deriverbar för x = 1?
Nej. Derivatans värde är olika
Du har alltså inte löst uppgiften. Försök igen.
Laguna skrev:Du har alltså inte löst uppgiften. Försök igen.
Ja. Jag har hittat ett litet slarv när jag försökte bestämma konstanterna a och b. Så rätt funktion är p(x)=2x^3-3x^2+x. Då är den både kontinuerlig och deriverbar
Ja, nu är det rätt.