bestäm en funktion
Bestäm en funktion f(x) sådan att linjen y = x + 2 är tangent till kurvan y = f(x) och f ′ (x) = x 4 .
Jag har gjort såhär men det känns som det är fel eftersom det är så enkelt:
vi vet att k=1
jag tog fram den primitiva funktionen av f´(x), vilket blev f(x)=(x^5)/5+C
f`(x)=1 ger x=+-1
sen om x=1
f(1)= 1^5/5+c=1+2 => c=14/15
om x=-1
f(-1)= -1^5/5+c?-1+2 => c=6/5
alltså är svaren om x=1 så blir f(x)= x^5/5+14/15
om x=-1 så blir f(x)=x^5/5+6/5
kan dett verklingen stämma?
Det har blivit fel i fallet då x=1
f(1)= 1^5/5+c=1+2 => 1/5 + c = 3 => c = 3 - 1/5 = 14/5, inte 14/15
Annars så är din lösning helt korrekt.
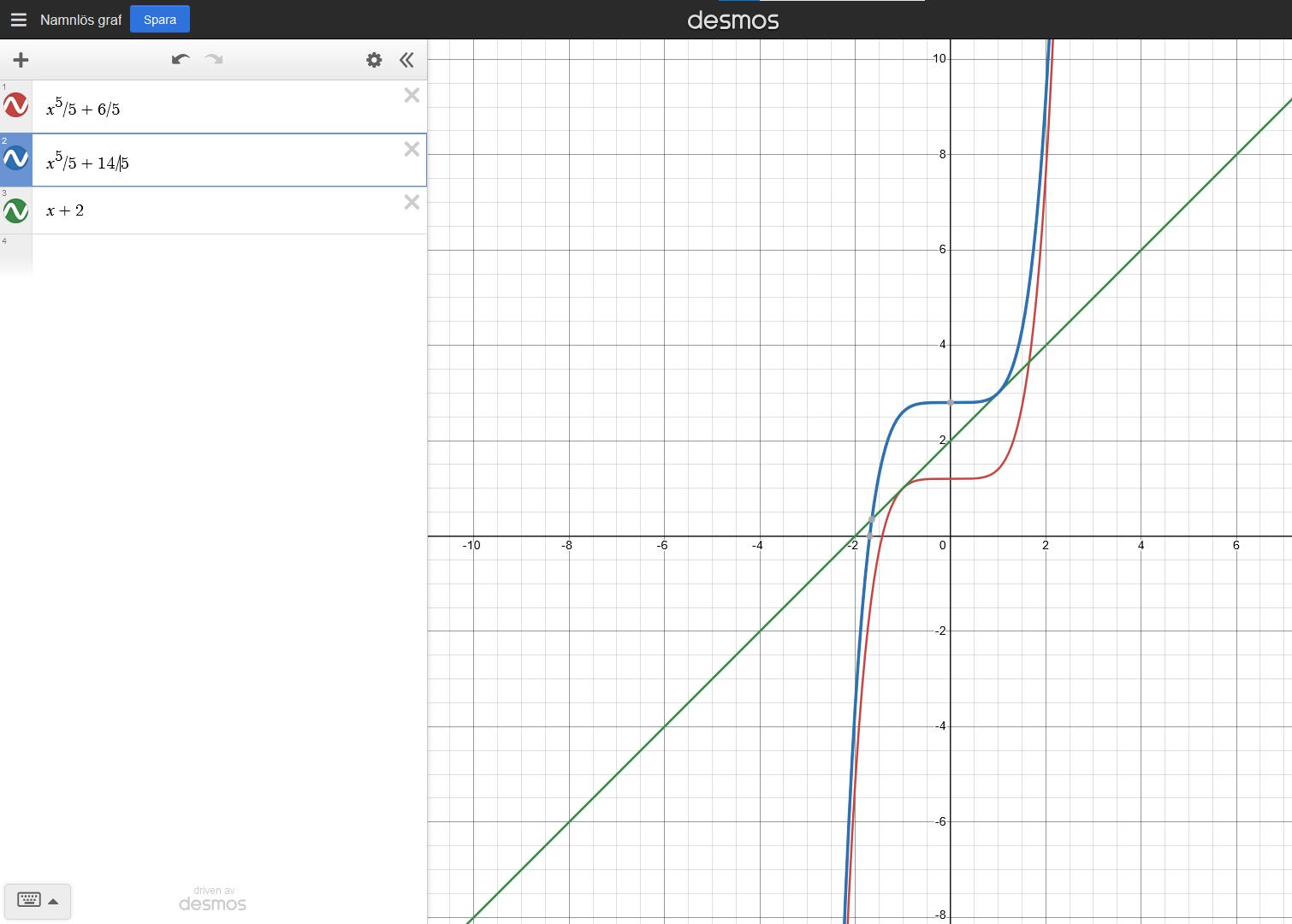
Om du känner dig osäker på om du har löst en uppgift korrekt så kan du alltid testa din lösning i desmos som i exemplet nedan: