Bestäm en ekvation för kurvan
Hej, jag skulle behöva hjälp med följande uppgift också. 
Jag har redan börjat räkna och har bestämt Amplituden. Men jag vet inte riktigt hur jag ska fortsätta.
Kan du bestämma perioden?
Börja med att rita upp det du vet. Läg uppdin bild här.
Jag vet att Ymax =5 när =120˚.
Ymin=1 när =300˚.
Jag antar då att grafen ser ut något liknande som den jag har ritat.
Rita i radianer istället! Annars kommer du inte att få fram ett svar som stämmer med facit.
Hur stor del av en period är det från ett maximum till ett minimum?
Från maximum till minimum är det halva perioden, i det här fallet 180˚ eller pi. Hela perioden blir då 360˚/2pi˚. Det jag vet nu är alltså att K=1, B=3 och A=2. Jag skulle inte säga att denna kurva är förskjuten i x-led.
Då blir ekvation y=2cosx+3. Stämmer det?
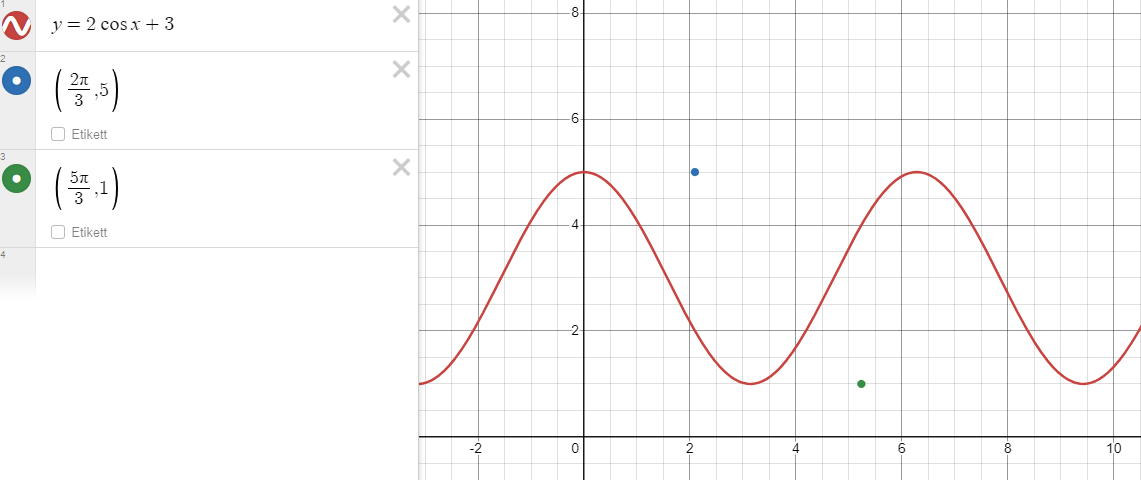
Punkterna du har fått i uppgiften ligger inte på den kurvan du har föreslagit. De ligger dock på rätt höjd vilket gör att du kan anta att din beräknade amplitud och förskjutning i y-led är rätt.
Det betyder då att mitt K-värde är fel. Om jag inte har förstått fel så är det ingen förskjutning på x-led.
Från Maximum till minimum är det en halv period, . Om en halv period är pi så är en hel period 2pi, vilket ger att K=1. Har jag missat något?
Du behöver bestämma om du ska använda sinus eller cosinus för att teckna din funktion. Förskjutningen kommer bero på vad du väljer.
Jag tänkte att det skulle bli en cosinus funktion men är osäker på hur jag ska gå tillväga för reda ut förskjutning i x-led.
Kurvan i inlägg #7 har förskjutningen 0 radianer. Det är uppenbarligen fel. Behöver du förskjuta kurvan åt höger eller vänster? Vad blir så tecknet på förskjutningen?
Jag har ritat både y=cosx och den andra.
Jag tänkte att cospi/2=0 i en vanlig cosinuskurva. Dock är cospi/2 inte 0. Så jag antog att kurvan var förskjuten 90˚ åt höger, vilket då kan ge 2cos(x-pi/2)+3. Detta stämmer inte helt dock.
Ett sätt är ju att testa dig fram i desmos/geogebra. Ett annat är att jämföra var du har maximum i de båda kurvorna, det är förskjutningen. Tänk på att inte blanda grader och radianer i ditt slutgiltiga uttryck bara
