Bestäm ekvationen till Tangenten (Matematik/Matte 3/Derivata)

Jag började tänkta att man skulle tillämpa derivatans definition

$\lim_{h \to 0} \frac{f (x + h) - f (x)}{h}$

Ja, så kan du göra.

När du har kommit fram till ett uttryck för derivatan f'(x) kan du sätta in x-värdet för att få ut tangentens lutning, dvs k-värdet i tangentens ekvation y = kx+m.

Men om du känner till deriveringsregeln för potensfunktioner så är det ett snabbare sätt.

Jag har inte lärt mig deriveringregler än. Jag är nyfiken hur man ska ställa upp funktionen mha av derivatans definition

OK bra.

Gör då en ''faktaruta" som består av uttrycken för f(x) och f(x+h).

Sätt sedan in detta i uttrycket för gränsvärdet och förenkla.

jag känner det ör svårt att förenkla mha av derivatans definition. Jag har inte f´rikitgt koll på det känner jag

Följ Yngves tips och visa hur långt du kommer, så kan vi hjälpa dig vidare.

Ta en sak i taget.

Börja med bråkets täljare, dvs f(x+h) - f(x).

Hur ser den ut när du skriver ut den?

Går den att förenkla?

Kanske faktorisera?

Smaragdalena skrev:
Följ Yngves tips och visa hur långt du kommer, så kan vi hjälpa dig vidare.

Du krånglar till det genom att ta för stora steg.

Ta ett steg i taget.

Du vet att f(x) = x²-1.

Hur ser då f(x+h) ut?

${(x + h)}^{2 ?}$

Nästan, men du glömmer termen -1

Du ska byta ut x mot x+h i uttrycket x²-1

ok, varför blir det här fel då ?

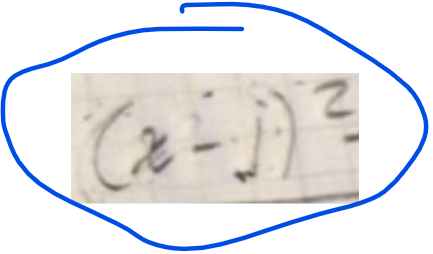
Det stämmer inte.

Är du med på följande?

Om f(x) = x²-1 så är

f(a) = a²-1?
f(7) = 7²-1?
f(kallekula) = kallekula²-1?

Nej, jag skrev

${(x - 1)}^{2}$

Arup skrev:
Nej, jag skrev

${(x - 1)}^{2}$

Ja, och det stämmer inte.

Svara gärna på frågorna i mitt förra svar.

ok, jag trodde näligen att man skulle kvadrera hela summan

OK, kan du då skriva vad f(x+h) blir?

$x^{2} + h ?$

Nej.

"Mallen" f(x) = x²-1 betyder att du ska ta det som står innanför funktionsparenteserna, kvadrera det och sedan subtrahera 1.

Därför blir

f(7) = 7²-1
1(a) = a²-1
f(b+c) = (b+c)²-1

Är du med på det?

Du borde ha skrivit (x+h)²-1. det är det uttryck man får om man byter ut x i x²-1 mot x+h.

Jag får förstår inte vad h står i detta fall

x+h är lite, lite mer än x. Vi vill låta h gå mot 0 så att vi får förändringen just i ögonblicket när x har rätt värde (0 i det här fallet, eftersom vi vill undersöka punkten (0,-1)).

Arup skrev:
Jag får förstår inte vad h står i detta fall

Förstår du att om f(x) = x²-1 så är f(a+b) = (a+b)²-1?

Yngve skrev:
Arup skrev:
Jag får förstår inte vad h står i detta fall

Förstår du att om f(x) = x²-1 så är f(a+b) = (a+b)²-1?

Borde inte då #15 vara rätt eftersom jag kavd3rar hela termen ?

Arup skrev:

Borde inte då #15 vara rätt eftersom jag kavd3rar hela termen ?

I svar #15 skriver du (x-1)².

Vilken del av f(x+h) är det tänkt att vara?

Jag tror att vi kommer snabbare framåt om du svarar på mina frågor.

Nej, i #15 skriver du (x-1)², inte x²-1 som funktionen är.

Jag upprepar frågan:

Yngve skrev:

Förstår du att om f(x) = x²-1 så är f(a+b) = (a+b)²-1?

Yngve var det så hör du menade ?

jag är fortfarande förvirrad om det ska vara

${(x + h)}^{2} - 1$

eller ${(x^{2} + h)}^{2} - 1$

Arup skrev:
jag är fortfarande förvirrad om det ska vara

${(x + h)}^{2} - 1$

Ja, så blir det om du sätter in x+h där det står x i x²-1.

eller ${(x^{2} + h)}^{2} - 1$

Nej, varför det?

Arup skrev:
Yngve var det så hör du menade ?

Ja, nu har du fått till uttrycket för f(x+h) rätt.

Men du tappar bort $\lim_{h\rightarrow0}$ på vägen.

=== Förslag på lösning ===

Utgå från derivatans definition

$f'(x)=\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}$

Faktaruta:

$f(x)=x^2-1$
$f(x+h)=(x+h)^2-1=x^2+2hx+h^2-1$

Sätt in detta i uttrycket:

$f'(x)=\lim_{h\rightarrow0}\frac{(x^2+2hx+h^2-1)-(x^2-1)}{h}=$

$=\lim_{h\rightarrow0}\frac{2hx+h^2}{h}=$

$=\lim_{h\rightarrow0}\frac{h(2x+h)}{h}=$

$=\lim_{h\rightarrow0}(2x+h)=2x$

Arup skrev:
jag är fortfarande förvirrad om det ska vara

${(x + h)}^{2} - 1$

eller ${(x^{2} + h)}^{2} - 1$

Det tror jag inte att du skulle vara om du följde mina tips och besvarade mina frågor.

eftersom x termen är redan i kvadrat från informationen

$x^{2} - 1$

oj jag glömde citera #31

Om du svarar på mina frågor så kan jag hjälpa dig att få rätsida på detta.

Vi börjar med ett enklare exempel.

Vilket/vilka av följande påståenden är du med på och vilket/vilka är du inte med på?

"Mallen" g(x) = 2x+5 innebär att man ska multiplicera det som står innanför funktionsparenteserna (dvs x) med 2 och sedan till det addera 5.
Om g(x) = 2x+5 så innebär der att g(a) = 2a+5, eftersom det som står innanför funktionsparenteserna (a) ska multipliceras med 2 och sedan ska man till det addera 5.
Om g(x) = 2x+5 så innebär det att g(a+b) = 2(a+b)+5, eftersom det som står innanför funktionsparenteserna (a+b) ska multipliceras med 2 och sedan ska man till det addera 5.
Om g(x) = 2x+5 så innebär det att g(x+b) = 2(x+b)+5, eftersom det som står innanför funktionsparenteserna (x+b) ska multipliceras med 2 och sedan ska man till det addera 5.
"Mallen" f(x) = x²-1 innebär att man ska kvadrera det som står innanför funktionsparenteserna (dvs x) och ssedan från det subtrahera 5.
Om f(x) = x²-1 så innebär det att f(a) = a²-1, eftersom det som står innanför funktionsparenteserna (a) ska kvadreras och sedan ska man från det subtrahera 1.
Om f(x) = x²-1 så innebär det att f(a+b) = (a+b)²-1, eftersom det som står innanför funktionsparenteserna (a+b) ska kvadreras och sedan ska man från det subtrahera 1.
Om f(x) = x²-1 så innebär det att f(x+b) = (x+b)²-1, eftersom det som står innanför funktionsparenteserna (x+b) ska kvadreras och sedan ska man från det subtrahera 1.
Om f(x) = x²-1 så innebär det att f(x+h) = (x+h)²-1, eftersom det som står innanför funktionsparenteserna (x+h) ska kvadreras och sedan ska man från det subtrahera 1.

========

EDIT - Korrigerade ett par skrivfel. Tack Laguna.

Arup skrev:
oj jag glömde citera #31

Hej Arup. Jag undrar bara om varför du kunde inte bara ta prim operationen av f(x). Varför valde du att använda dig av derivatans definition? Det skulle bli så mycket lättare. Prim operationen innebär bara att ta derivatan av f(x)

shkan skrev:
Arup skrev:
oj jag glömde citera #31

Hej Arup. Jag undrar bara om varför du kunde inte bara ta prim operationen av f(x). Varför valde du att använda dig av derivatans definition? Det skulle bli så mycket lättare. Prim operationen innebär bara att ta derivatan av f(x)

läs inlägg #4

Arup skrev:
shkan skrev:
Arup skrev:
oj jag glömde citera #31

Hej Arup. Jag undrar bara om varför du kunde inte bara ta prim operationen av f(x). Varför valde du att använda dig av derivatans definition? Det skulle bli så mycket lättare. Prim operationen innebär bara att ta derivatan av f(x)

läs inlägg #4

Vänta, du vet inte hur man tar derivatan av (x^2 -1)? Det är ju bara derivatan av x^2 - derivatan av 1. Derivatan av en konstant är alltid noll, och derivatan av x^2 är ju bara 2x

Annars kan du tänka dig så här: av f(x) så är punkten (0, -1) en extrempunkt (minimipunkt). Detta innebär att tangenten vid punkten är en konstantlinje, dvs y = m. Nu ska du bara hitta m. Det kan du veta genom att förstå att tangentens värde vid x= 0 är -1.

jag förstår

$\frac{d x}{d y} (x^{n}) = n \times x^{n - 1}$

Arup skrev:
jag förstår

$\frac{d x}{d y} (x^{n}) = n \times x^{n - 1}$

Inte dx/dy, det är dy/dx.

Egentligen d/dx.

Yngve skrev:
Egentligen d/dx.

Ja faktiskt. Däremot menar jag att y = x^n :)

shkan skrev:
Annars kan du tänka dig så här: av f(x) så är punkten (0, -1) en extrempunkt (minimipunkt). Detta innebär att tangenten vid punkten är en konstantlinje, dvs y = m. Nu ska du bara hitta m. Det kan du veta genom att förstå att tangentens värde vid x= 0 är -1.

Nja, varför skulle man kunna utgå från att punkten (0,-1) är en extrempunkt? Det är klart att man kan se att den är det om man ritar upp kurvan, eller om man tar fram symmetrilinjen för funktionen, men då mpste man göra detta först!

Smaragdalena skrev:
shkan skrev:
Annars kan du tänka dig så här: av f(x) så är punkten (0, -1) en extrempunkt (minimipunkt). Detta innebär att tangenten vid punkten är en konstantlinje, dvs y = m. Nu ska du bara hitta m. Det kan du veta genom att förstå att tangentens värde vid x= 0 är -1.

Nja, varför skulle man kunna utgå från att punkten (0,-1) är en extrempunkt? Det är klart att man kan se att den är det om man ritar upp kurvan, eller om man tar fram symmetrilinjen för funktionen, men då mpste man göra detta först!

Bara en lösningsalternstiv, inte behöver att Arup ska göra exakt denna metod

Yngve skrev:
Om du svarar på mina frågor så kan jag hjälpa dig att få rätsida på detta.

Vi börjar med ett enklare exempel.

Vilket/vilka av följande påståenden är du med på och vilket/vilka är du inte med på?

"Mallen" g(x) = 2x+5 innebär att man ska multiplicera det som står innanför funktionsparenteserna (dvs x) med 2 och sedan till det addera 5.

Om g(x) = 2x+5 så innebär der att g(a) = 2a+5, eftersom det som står innanför funktionsparenteserna (a) ska multipliceras med 2 och sedan ska man till det addera 5.

Om g(x) = 2x+5 så innebär det att g(a+b) = 2(a+b)+5, eftersom det som står innanför funktionsparenteserna (a+b) ska multipliceras med 2 och sedan ska man till det addera 5.

Om g(x) = 2x+5 så innebär det att g(x+b) = 2(x+b)+5, eftersom det som står innanför funktionsparenteserna (x+b) ska multipliceras med 2 och sedan ska man till det addera 5.

"Mallen" f(x) = x²-1 innebär att man ska kvadrera det som står innanför funktionsparenteserna (dvs x) och ssedan från det subtrahera 5.

Om f(x) = x²-1 så innebär det att f(a) = a²-1, eftersom det som står innanför funktionsparenteserna (a) ska kvadreras och sedan ska man från det subtrahera 1.

Om f(x) = x²-1 så innebär det att f(a+b) = (a+b)²-1, eftersom det som står innanför funktionsparenteserna (a+b) ska kvadreras och sedan ska man från det subtrahera 1.

Om f(x) = x²-1 så innebär det att f(x+b) = (x+b)²-1, eftersom det som står innanför funktionsparenteserna (x+b) ska kvadreras och sedan ska man från det subtrahera 1.

Om f(x) = x²-1 så innebär det att f(x+h) = (x+h)²-1, eftersom det som står innanför funktionsparenteserna (x+h) ska kvadreras och sedan ska man från det subtrahera 1.

========

EDIT - Korrigerade ett par skrivfel. Tack Laguna.

Jag är med på alla punkter fram till 8

Tack för att du svarar på frågorna!

Är du alltså med på 1-7 men inte på 8 och 9?

ja

OK då tittar vi närmare på punkt 8.

Vi har ett funktionsuttryck som lyder f(x) = x²-1 och vi vill ta fram ett uttryck för f(x+b).

Jag ska nu på ett annat sätt försöka visa varför f(x+b) = (x+b)²-1.

=========

Vi börjar med att göra en substitution där vi sötter y = x+b.

Då ska vi ta fram ett uttryck för f(y).

Eftersom f(x) = x²-1 så är f(y) = y²-1.

(Detta är exakt samma sak som i punkt #6.)

=========

Nu byter vi tillbaka från y till x+b och vi får då f(x+b) = (x+b)²-1.

Hur kändes det, var det enklare att se då?

ja

OK bra.

Är du då med på punkt 8?

japp

OK, bra. Är du då även med på punkt 9?

Om du är med på att f(x+h) = (x+h)²-1 så kan du gärna försöka lösa uppgiften med hjälp av derivatans h-definition, det är bra träning.

Börja då gärna enligt följande:

$f'(x)=\lim_{h\rightarrow0}\frac{T}{h}$ , där $T=f(x+h)-f(x)$

Sätt nu upp och förenkla uttrycket för $T$ med hjälp av en "faktaruta" bestående av ett uttryck för f(x) och ett uttryck för f(x+h).

Sätt sedan in detta förenklade uttryck i formeln för f'(x).

jag fick svaret till 2x

Bra! Det stämmer att f'(x) = 2x.

Om du vill ha kommentarer på din lösning så får du visa den.

======

Vill du ha mer hjälp med att lösa själva uppgiften?

jag kan lägga upp en bild och sen kan du ge mig feedback på lösningen

OK det gör jag gärna.

Nej, nu använder du T fel.

Anledningen att använda T är att kunna förenkla ändringskvotens täljare separat, vid sidan av.

Och därmed slippa behöva göra det i ett komplicerat limes-uttryck.

Så hör:

$f'(x)=\lim_{h\rightarrow0}\frac{T}{h}$ , där $T=f(x+h)-f(x)$ .

===== Faktaruta =====

$f(x)=x^2-1$

$f(x+h)=(x+h)^2-1=x^2+2hx+h^2-1$

==========

Det ger oss

$T=(x^2+2hx+h^2-1)-(x^2-1)=2hx+h^2=$

$=h(2x+h)$

Insatt i derivatans h-definition får vi nu alltså

$f'(x)=\lim_{h\rightarrow0}\frac{h(2x+h)}{h}=$

$=\lim_{h\rightarrow0}(2x+h)=2x$

Yngve när du sätter T menar du båda funktionerna dvs f(x) och f(x+h) ?

Är det inte lättare att använda två bokstäver i det här fallet Y och T, där T=f(x+h) och Y=f(x).

Arup skrev:
Yngve när du sätter T menar du båda funktionerna dvs f(x) och f(x+h) ?

Ja, jag menar att T = f(x+h) - f(x)

Är det inte lättare att använda två bokstäver i det här fallet Y och T, där T=f(x+h) och Y=f(x).

Så kan du göra om du vill, men jag tror inte att det är lättare

=======

Alltså, du behöver inte använda T och/eller Y om du inte vill.

Här är en mer "pang på"-lösning som inte involverar vare sig T eller Y:

$f'(x)=\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}=$

$=\lim_{h\rightarrow0}\frac{((x+h)^2-1)-(x^2-1)}{h}=$

$=\lim_{h\rightarrow0}\frac{(x^2+2hx+h^2-1)-(x^2-1)}{h}=$

$=\lim_{h\rightarrow0}\frac{x^2+2hx+h^2-1-x^2+1}{h}=$

$=\lim_{h\rightarrow0}\frac{2hx+h^2}{h}=$

$=\lim_{h\rightarrow0}\frac{h(2x+h)}{h}=$

$=\lim_{h\rightarrow0}(2x+h)=$

$=2x$

===========

Det går alltså alldeles utmärkt att köra "direkt", bara man har koll på alla termer och faktorer i det komplicerade uttrycket.

I det här fallet var funktionen f(x) ganska enkel, men om f(x) är mer komplicerad så kan det bli väldigt rörigt och dwt är då lätt att trassla in sig med denna metod.

Då är metoden med att uttrycka och förenkla täljaren vid sidan av (t ex. i form av T = f(x+h)-f(x)), en bra variant.

Om man inte vill behöva skriva $\lim_{h\rightarrow0}$ så många gånger:

$f'(x)=\lim_{h\rightarrow0}\frac{T}{h}$ där $T = f(x+h)-f(x)$

$T=((x+h)^2-1)-(x^2-1))=(x^2+2hx+h^2-1)-(x^2-1)=x^2+2hx+h^2-1-x^2+1=2hx+h^2$

$f'(x)=\lim_{h\rightarrow0}\frac{h(2x+h)}{h}=\lim_{h\rightarrow0}(2x+h)=2x$

Ett annat sätt är att skriva så här:

========

$f'(x)=\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}$

Eftersom $f(x)=x^2-1$ så är $f(x+h)=(x+h)^2-1=$

$=x^2+2hx+h^2-1$

Vi tittar nu endast på differenskvotens täljare, där vi har att

$f(x+h)-f(x)=$

$=(x^2+2hx+h^2-1)-(x^2-1)=$

$=x^2+2hx+h^2-1-x^2+1=$

$=2hx+h^2=h(2x+h)$

Nu sätter vi in detta i derivatans definition och vi får då

$f'(x)=\lim_{h\rightarrow0}\frac{h(2x+h)}{h}=$

$=\lim_{h\rightarrow0}(2x+h)=2x$

========

Vi kan alltså använda samma metod, att formulera och förenkla täöljaren separat, utan att blanda in ett $T$ .

Men då måste vi, som här, tydligt skriva vad vi gör.

Yngve hur skulle du lösa frågan mha av en "faktaruta" ?

Arup skrev:
Yngve hur skulle du lösa frågan mha av en "faktaruta" ?

Jag har gulmarkerat "faktarutan" här:

så du använde inte T idet här fallet.

Det stämmer.

Att kalla täljaren T och att använda en faktaruta är två helt oberoende saker.

Du kan välja att använda båda, ena eller ingen av dessa.

Jag har visat några olika sätt att beskriva uträkningen.

Det finns fler, mer eller mindre komplicerade.

Välj en metod du känner dig bekväm med.

Jämför gärna dessa lösningsförslag med de i din andra tråd om derivatans h-definition.

Du kommer att se att principen är densamma:

Ställ upp uttrycket för f'(x)
Ta fram uttryck för f(x) och f(x+h) ("faktarutan")
Ställ upp och förenkla f(x+h)-f(x)
Ersätt täljaren I derivatans definition med detta förenklade uttryck
Förkorta med h om det går.
Låt h gå mot 0.
Klart.