Bestäm ekvation för plan som går genom linje och punkt

När ett plan går genom en linje impliceras detta: 

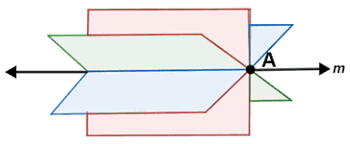
Är du med på det?

Nej, det var jag nog inte med på. Måste linjen gå genom mitten av planet? Eller jag förstår inte riktigt hur jag ska tolka bilden.

Nej, planet är ju oändligt i rummet. 

Ja, jag är med på att planets utbredning är oändlig. Så här tänker jag att det ser ut (den oranga linjen):

Isåfall finns det oändligt med plan som uppfyller kraven. Ser du varför? Det ska vara ett bestämt plan. 

Ser du varför?

För att man kan vrida dem runt skärningspunkten?

Ja, precis. 

Då är jag lite lost på hur man ska åtgärda det problemet. Problemet kvarstår väl om linjen ligger i planet, så vilka andra alternativ finns kvar? Alltså här finns det väl också oändligt många plan, bara att man vrider dem runt linjen istället för runt en punkt (vilket kanske var det du ville visa?).

Nej, jag ville visa att om linjen ligger i planet finns det endast ett plan som också går igenom punkten. Sätt ut punkten på ett valfritt ställe i bilden i inlägg 2 så ser du att endast ett plan kan nå denna punkt. 

För lösningsmetod behöver du hitta normalen till planet genom att ta fram en godtycklig punkt på linjen, beräkna en vektor mellan den punkten och den givna punkten i uppgiften och kryssa denna vektor med riktningsvektorn för linjen. Då får du normalen (a,b,c) som du direkt kan sätta in i ax+by+cz+d=0 och därefter använda punkten igen eller göra allt i ett steg genom a(x-x1)+b(y-y1)+c(z-z1)=0 där (x1,y1,z1) är en punkt i planet. 

Nej, jag ville visa att om linjen ligger i planet finns det endast ett plan som också går igenom punkten. Sätt ut punkten på ett valfritt ställe i bilden i inlägg 2 så ser du att endast ett plan kan nå denna punkt. 

Så länge punkten inte också ligger på linjen då, eller hur?

Ja, exakt. Då når ju alla plan både linjen och punkten och vi har inget problem längre. Men man ser ju direkt att punkten inte ligger på linjen. 

Jag kommer inte riktigt någonstans. Jag har försökt göra en liten ritning:

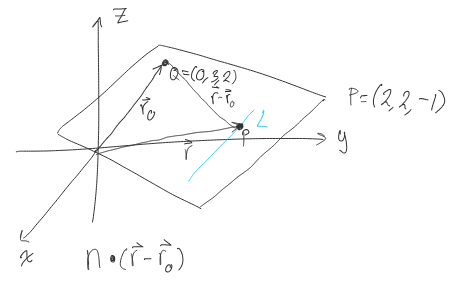
Jag har kommit fram till att linjen på vektorform kan skrivas $\displaystyle \vec{r}=\left( 2 ,2,-1 \right) + \left( 2,1,-1 \right) t$

Det betyder att min punkt $P$ i bilden är $P = (2,2,-1)$ (eller vi låter punkten vara den). Sedan är jag lite lost. Har jag tagit fram något som är användbart här eller är jag ute och cyklar igen? 

Jag har en känsla av ett sådan här uppgift är extremt standard men jag blir inte klokare av att läsa i kurslitteraturen. Fy fasiken vad jag ogillar Adams stil. Han bara ritar en bild och så tycker han det räcker, men jag behöver text också 🤡

Jag förstår inte riktigt din bild. $\vec{r}$ bör vara riktad åt samma håll som linjen. Detta är min bild: 

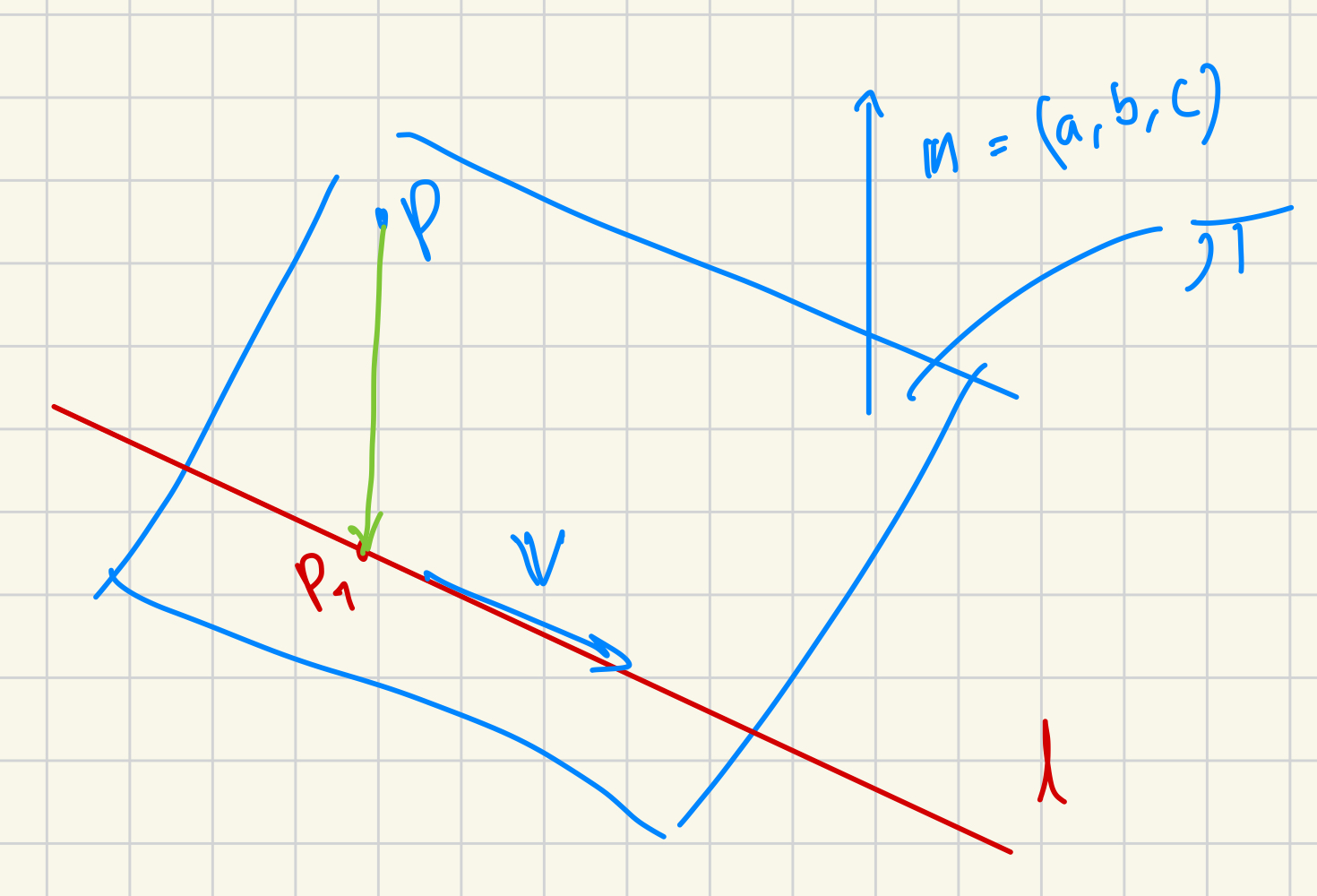
(klippte ut den från resten av min lösning, därför lite oklara beteckningar)

Varför bör den vara det? Jag tänkte att $\vec{r}\left(t\right)$ skulle vara lägesvektorn från origo till alla punkter på linjen. Har jag missuppfattat det?

naytte skrev:

Varför bör den vara det? Jag tänkte att $\vec{r}\left(t\right)$ skulle vara lägesvektorn från origo till alla punkter på linjen. Har jag missuppfattat det?

Så tolkar jag det också.

För att ta oss tillbaka till ursprungsproblemet: Ett plan kan definieras av två linjärt oberoende vektorer som spänner upp planet. Eftersom att planet ska gå genom linjen måste riktningskoefficienten för denna linje vara den ena vektorn som spänner upp planet. Eftersom att även punkten ska ligga i planet kan vektorn som går mellan linjen och punkten vara den andra vektorn.

Nu är det fritt fram att skriva om det framtagna planet på valfri form.

Eftersom att planet ska gå genom linjen måste riktningskoefficienten för denna linje vara den ena vektorn som spänner upp planet.

Vad avser vi med riktningskoefficienten här? Vektorn framför $t$:et i linjens vektorform?

naytte skrev:

Eftersom att planet ska gå genom linjen måste riktningskoefficienten för denna linje vara den ena vektorn som spänner upp planet.

Vad avser vi med riktningskoefficienten här? Vektorn framför $t$:et i linjens vektorform?

Stämmer bra

naytte skrev:

Varför bör den vara det? Jag tänkte att $\vec{r}\left(t\right)$ skulle vara lägesvektorn från origo till alla punkter på linjen. Har jag missuppfattat det?

Ja, det stämmer. Jag kollade fel på din bild, såg ut som du ritade r längs y på något konstigt sätt, vet ej varför jag trodde det.

Aaaah, jag tror det klickade för mig nu! Jag tror jag har en lösning nu:

Låt $\displaystyle P=\{ (x,y,z)\in\mathbb{R}^3:ax+bx+cz+d=0\}$. Vi har att $Q=(0,3,2)$ ligger i planet. Vi skriver sedan linjen på vektorform:

$\displaystyle \vec{r}\left(t\right)=\left(2,2,-1\right)+\left(2,1,-1\right)t$

Vi väljer sedan punkten $A=(2,2,-1)$ på linjen. Riktningsvektorn $\displaystyle \vec{u} =\left(2,1,-1\right)$ ligger i planet eftersom linjen måste ligga i planet. Dessutom ligger vektorn $\displaystyle \vec{QA}$ i planet, och definieras enligt: $\vec{QA} = \left(-2,1,3\right)$. Om vi kryssar dessa vektorer får vi en normal till planet:

$\displaystyle \vec{QA} \times\vec{u} = \left(-2,1,3\right) \times\left(2,1,-1\right) = \left(-4,4,-4\right)$

Planet med denna normal kommer ha ekvationen:

$\displaystyle -4x+4y-4z=4 \iff x-y+z = -1$

Det jag inte klockade var varför man skulle ta kryssprodukten mellan just dessa vektorer, men det slog mig nu att det inte spelar någon roll vilka vektorer man kryssar så länge båda ligger i planet. Hela målet är ju att få någon normal, det spelar ingen roll vilken. Stämmer det?

Mycket bra!

naytte skrev:

Det jag inte klockade var varför man skulle ta kryssprodukten mellan just dessa vektorer, men det slog mig nu att det inte spelar någon roll vilka vektorer man kryssar så länge båda ligger i planet. Hela målet är ju att få någon normal, det spelar ingen roll vilken. Stämmer det?

Faktum är att samtliga normaler kommer vara identiska upp till en faktor (denna faktor kan även vara negativ). Med detta menar jag att riktningen för alla normaler är densamma (möjligen motriktad om faktorn framför är negativ).

När du väl har hittat normalen (-4,4,-4) erhåller du planets ekvation -4x+4y-4z+d=0 och därifrån är det bara att stoppa in valfri punkt på planet för att erhålla d. T.ex punkten (0,3,2) ger 0+12-8+d=0 vilket ger d=-4.

Tillägg: 20 okt 2024 23:05

Självklart gäller det att -4x+4y-4z-4=0 är samma plan som -x+y-z-1=0.

Vi kunde även normerat om normalvektorn till (-1,1,-1) innan vi bestämde d och därmed hade vi direkt fått d=-1.

Är det alltid så att koefficienterna $a,b,c$ i planets ekvation:

$\displaystyle ax+by+cz+d = 0$ 

är komposanterna i (en) normal(en) till planet?

naytte skrev:

Är det alltid så att koefficienterna $a,b,c$ i planets ekvation:

$\displaystyle ax+by+cz+d = 0$ 

är komposanterna i (en) normal(en) till planet?

Yes!

Kvällens sista uppgift för dig är att ta reda på varför ;)

Är det eftersom planet kan tänkas vara mängden av alla vektorer som är ortogonala mot normalen? Så för en given punkt $P=(x_0, y_0, z_0)$ och en annan punkt $Q = (x_1, y_1, z_1)$, så kommer vektorn $\vec{PQ}$ ligga i planet omm $\displaystyle \vec{PQ}\bullet\vec{n} = 0$, alltså ska:

$\displaystyle a(x_1-x_0)+b(y_1-y_0)+c(z_1-z_0) = 0$

där $\vec{n} = \left(a,b,c\right)$

Snyggt!

Ser bra ut, låter som ett fläckfritt argument.

Ett annat sätt att hitta normalen till planet är helt enkelt att ta gradienten av planet:
$\nabla (ax+by+cz+d)=(a,b,c)$

Detta kommer ni förstå senare i vektoranalysen!

Tack så hemskt mycket till er båda!

Calle_K skrev:

Ser bra ut, låter som ett fläckfritt argument.

Ett annat sätt att hitta normalen till planet är helt enkelt att ta gradienten av planet:
$\nabla (ax+by+cz+d)=(a,b,c)$

Detta kommer ni förstå senare i vektoranalysen!

Naaaajs, linjär algebra är stört tillfredsställande. Allt hänger så väldigt bra ihop.😃