Bestäm det minsta värde ∣ z ∣ kan anta.

Vi har förhållandet att $xy = 1$. Kan du skriva upp hur man beräknar $|z|$?

Minsta värde innebär ofta att hitta minimipunkten på någon funktion

$\left|z\right| =\sqrt{x^2+y^2} = \sqrt{x^2+{\left(\frac{1}{x}\right)}^2}=\sqrt{x^2+x^{-2}}$

Något sådant kanske? Blir detta en funktion som ska deriveras?

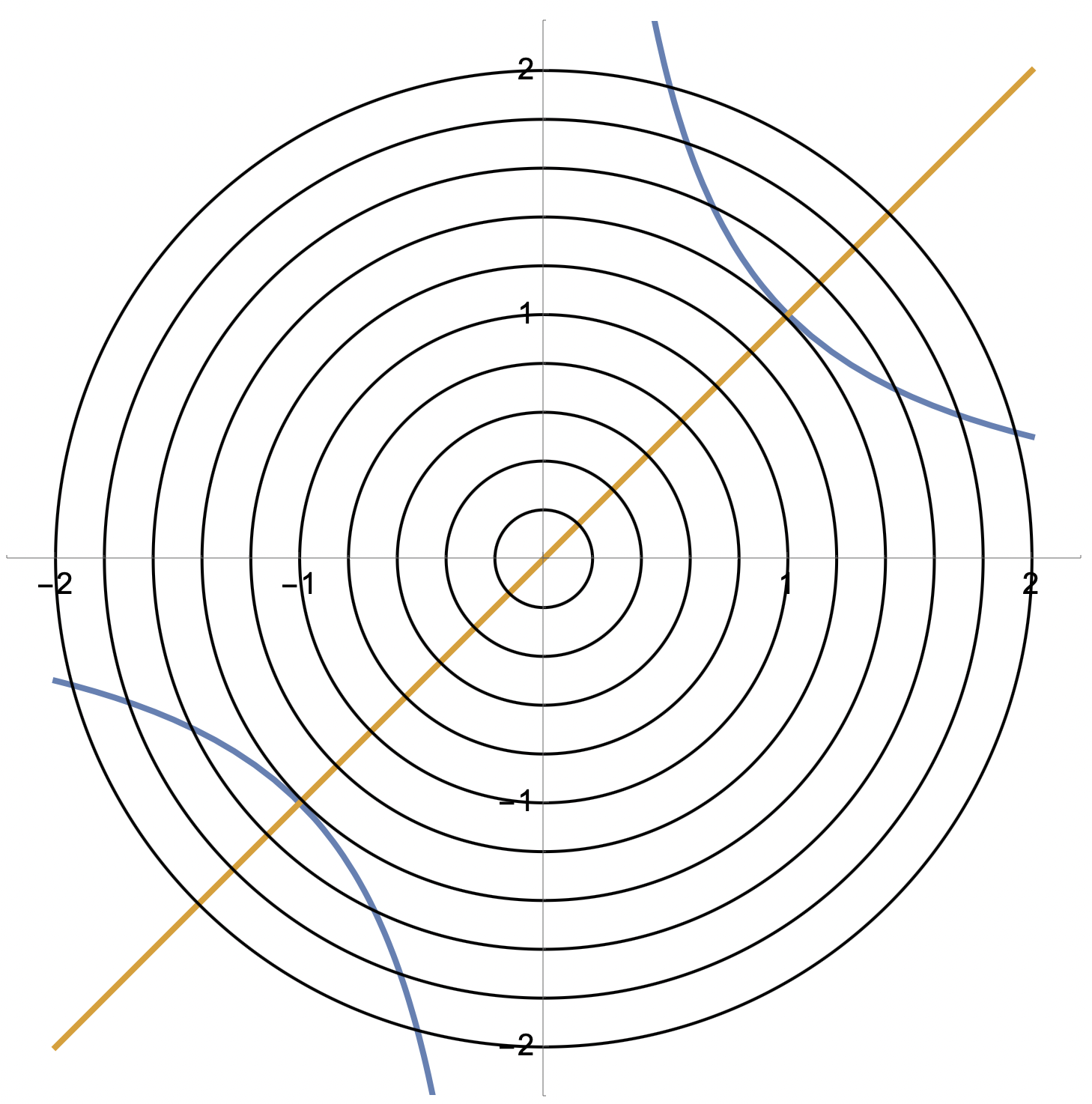
Den första hade jag nog löst med en bild;

Problemet är att man ej får använda något digitalt verktyg

Anonym_15 skrev:

Problemet är att man ej får använda något digitalt verktyg

Det behövs ej. xy=1 eller y=1/x är en välkänd kurva som går genom (1,1) och avståndet |z| är i praktiken cirkelradier. Du skissar lätt denna bild för hand och inser vad minsta radien är.

Låt oss säga att jag inte vet hur kurvan ser ut innan. Hur kan jag derivera, hitta min punkten och verifiera denna på ett smidigt sätt?

Den andra frågan kan också bestämmas med en bild

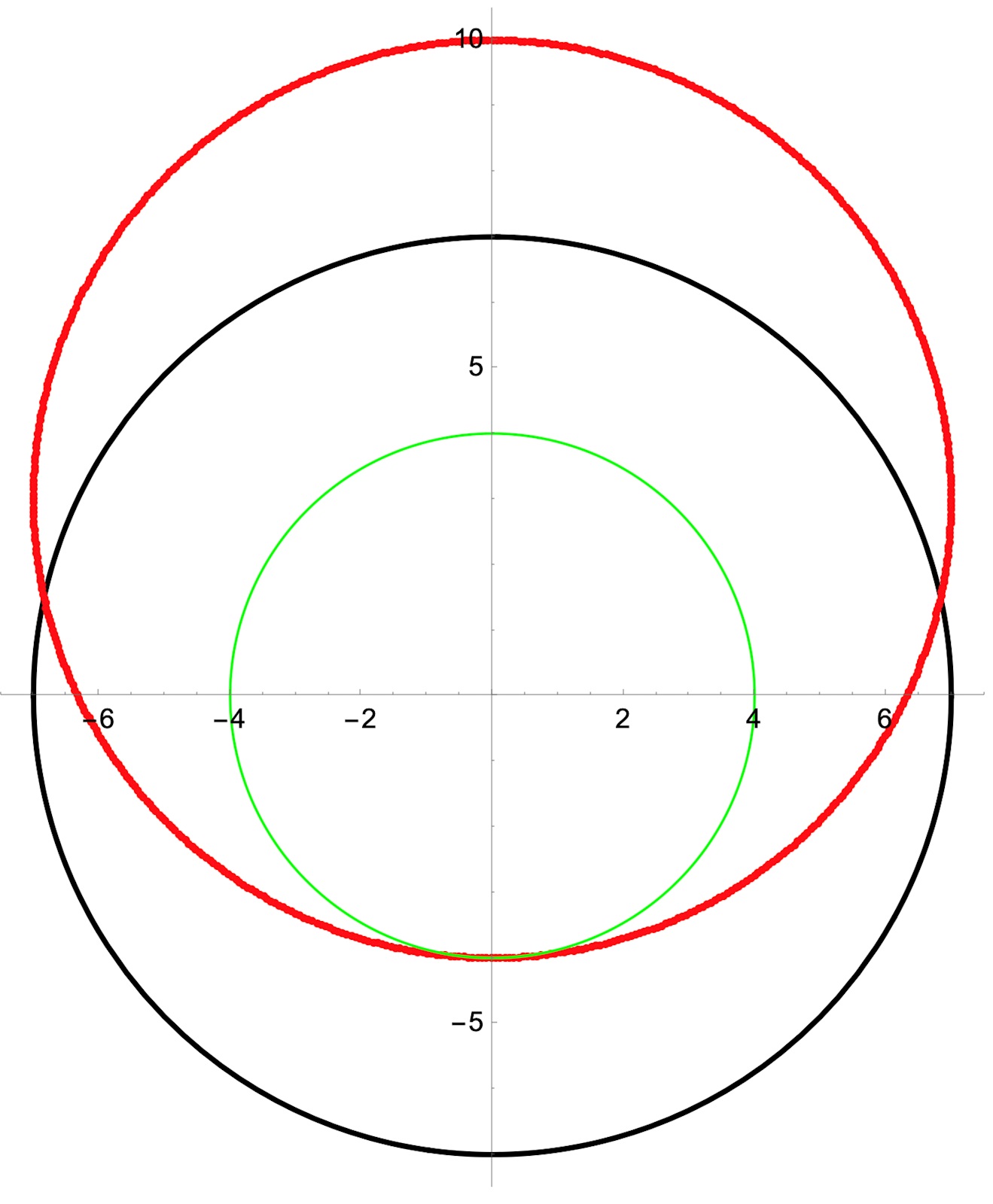
Svart cirkel är |z_2|=7 och röd cirkel är svart cirkel förflyttad z1=+3i, dvs +3 steg i vertikalled. Detta är punkterna z_2+z_1. Minsta avståndet från origo är 4 (punkten -4i).

Anonym_15 skrev:

Låt oss säga att jag inte vet hur kurvan ser ut innan. Hur kan jag derivera, hitta min punkten och verifiera denna på ett smidigt sätt?

#3 ser bra ut

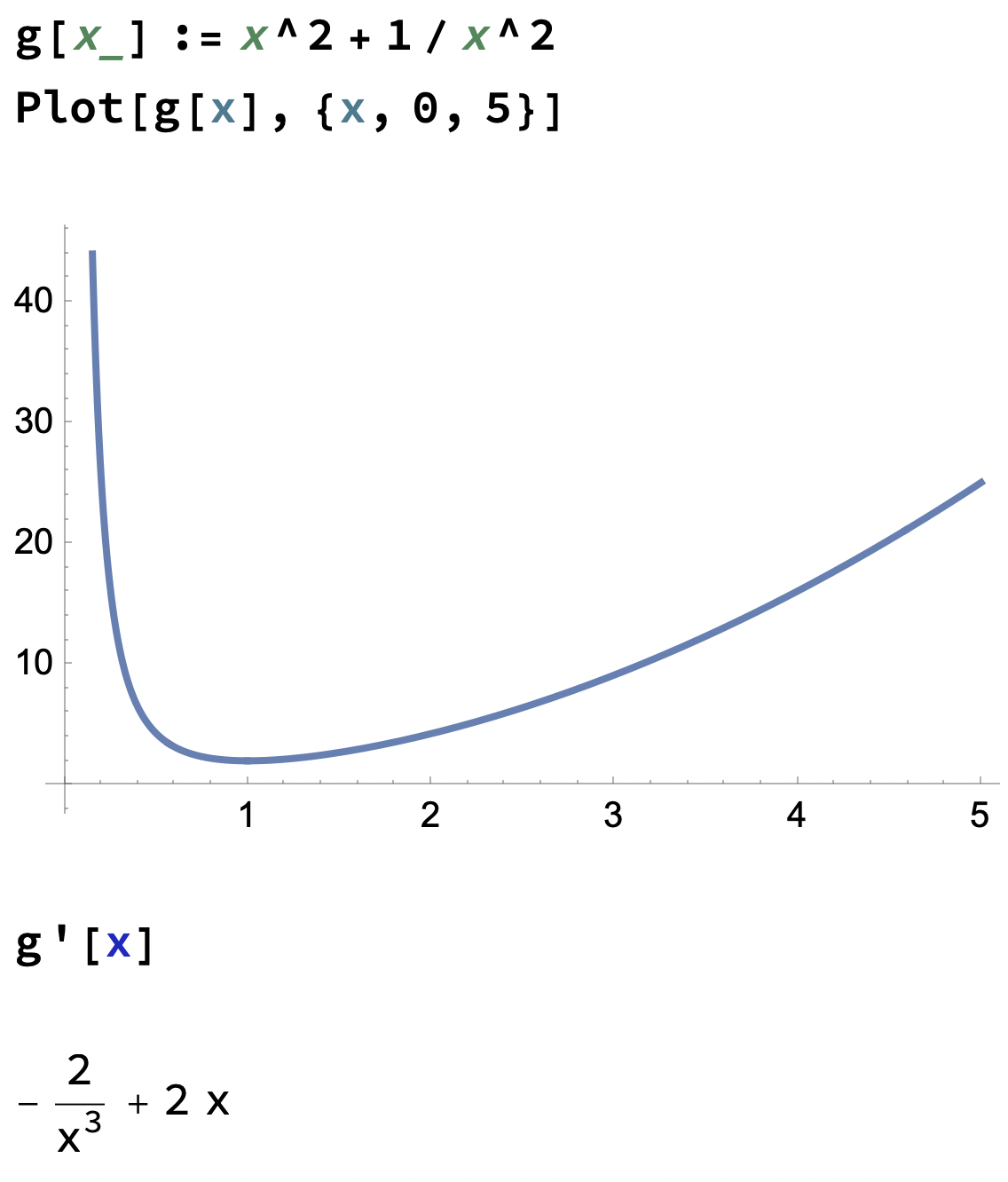
Du ser direkt att x=1 löser ekvationen g'=0

Men här används väl också miniräknare?

Anonym_15 skrev:

Men här används väl också miniräknare?

Nej, "huvudräkning" och med papper och penna.

Ok, men om jag har förstått rätt ska man vid sådana frågor försöka skriva konjugatet som en funktion, derivera och hitta minimipunkten? Eller finns det något annat sätt? Jag tänkte själv på cosinussatsen

Anonym_15 skrev:

Ok, men om jag har förstått rätt ska man vid sådana frågor försöka skriva konjugatet som en funktion, derivera och hitta minimipunkten? Eller finns det något annat sätt? Jag tänkte själv på cosinussatsen

Jag tror de i detta moment mera vill påvisa en förståelse för det komplexa talplanet och vad |z| betyder för punkter. Analytiska metoder går men det är lite over-kill. Men, alla medel är tillåtna. Det finns inga dåliga sätt om de ger rätt svar.

Anonym_15 skrev:

Hej, har stött på två frågor som liknar varandra och undrar vilken metod jag kan använda för att lösa dessa:

När jag tänker på "minsta värde" tänker jag att cos eller sin ska användas på något sätt, men vet ej hur. 

Du kanske tänkte något så här?

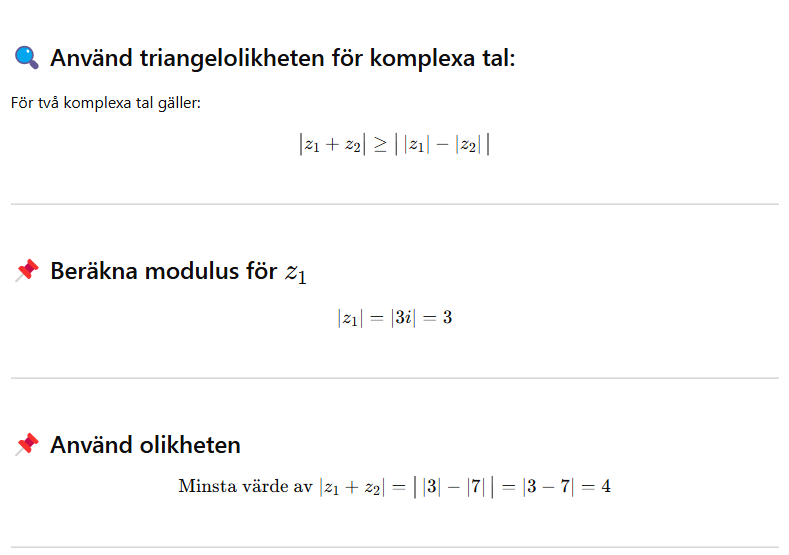
Går det att tänka så här?