Bestäm den punkt på kurvan y=f(x) som ligger närmast origo

Jag har fastnat på optimeringsdelen. Har ritat ut tangenten och försökt skriva ut samband som bara blir knasiga. Avståndsformeln blir ju d=sqrt(x2+y2) ty origo. Funderade på om jag kunde istället använda pytagoras sats kombinerat med att jag då har lutningen på kurvan (tangenten) men det blir också konstigt.

Varför har du stoppat in tangentens ekvation istället för kurvans i funktionen för avstånd?
Och din derivering av har blivit lite fel. Se över den igen!
naytte skrev:Varför har du stoppat in tangentens ekvation istället för kurvans i funktionen för avstånd?
Och din derivering av har blivit lite fel. Se över den igen!
Hur är deriveringen fel? Menar du att jag skulle derivera inversen istället?
Hoppsan, jag läste den raden fel!
Men den andrs frågan kvarstår.
naytte skrev:Hoppsan, jag läste den raden fel!
Men den andrs frågan kvarstår.
Ser detta bättre ut?
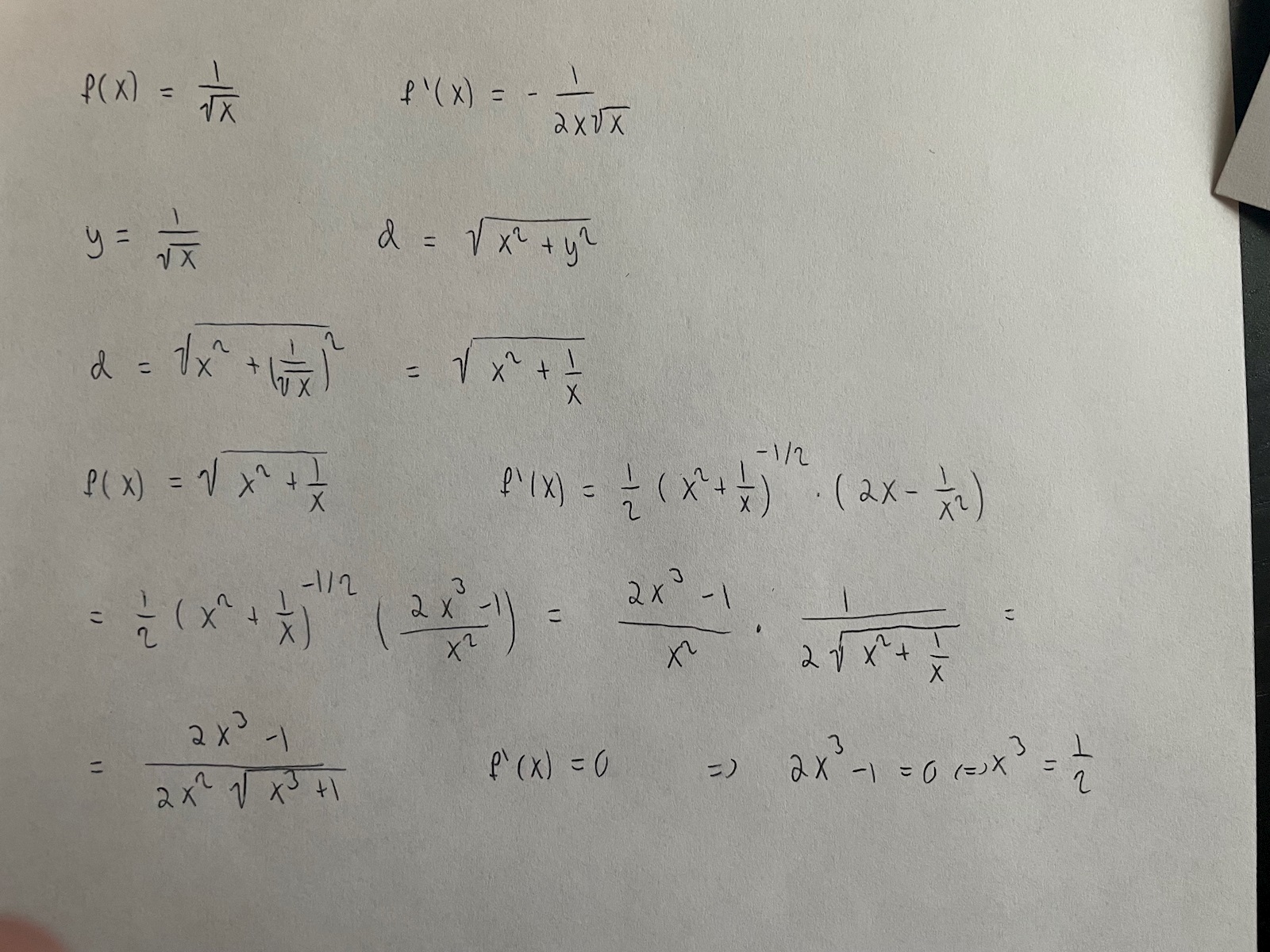
Ser rätt ut.
Jag hade dock stannat här:
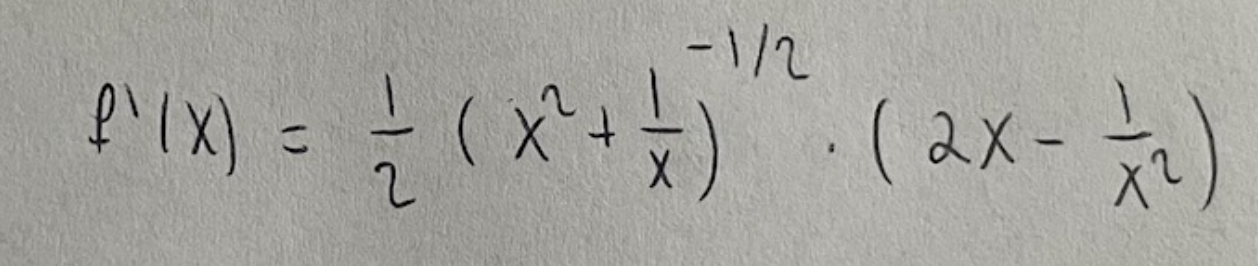
och fortsatt här
![]()
Ju mindre man skriver, ju mindre risk att man skriver fel, och räknar fel.
Ditt nästa steg är att lösa f'(x)=0 och då

är väldefinerad för x>0 och positiv kan den anses vara en positiv konstant, säg 1.
Ev. teckenstudium för att verifiera att det är minimum senare påverkas ej av denna *positiva* konstant.
Dessutom är 2x-1/x^2 strängt växande (det är en summa av 2 strängt växande funktioner då x>0) varför funnet nollvärde måste vara en lokal minimipunkt.


