Bestäm den maximala arean
Hej, har länge försökt förstå varför inte min metod fungerar till följande uppgift:
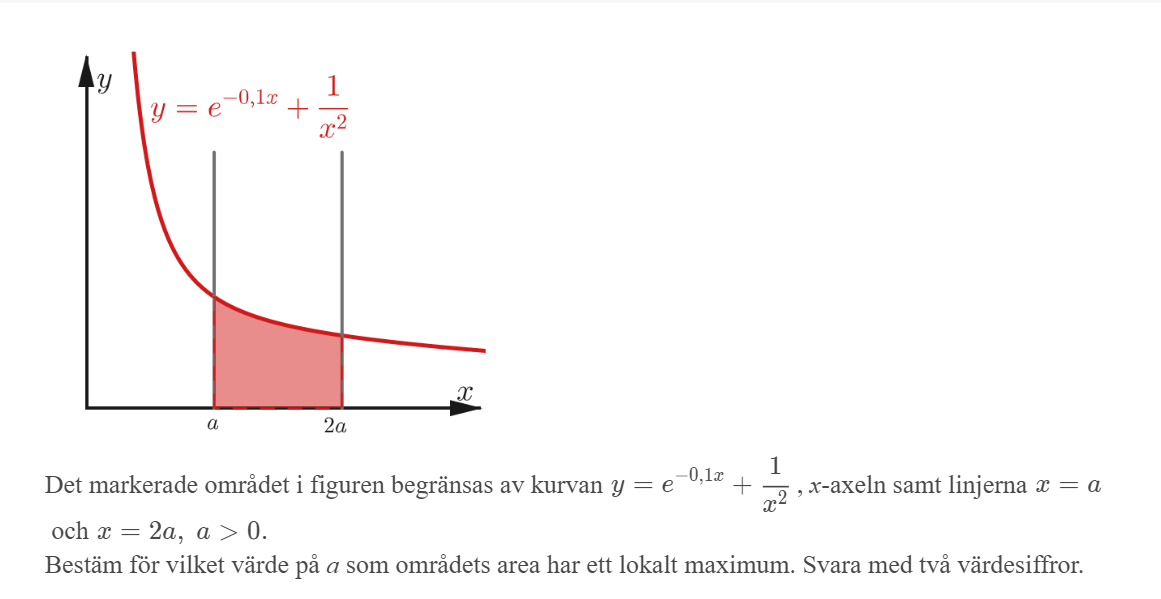
Jag tänker följande:
Arean kan beskrivas med: F(2a) - F(a). Arean kan skrivas som en funktion med a som oberoende variabel.
Om vi ska hitta areans maximala värde ska funktionen deriveras. Dvs.
F'(a) = F'(2a) - F'(a) = f(2a) - f(a). Jag skriver in detta i min grafräknare för att hitta de värden på a som ger derivatan värdet noll men får då endast fram ett negativt värde. Detta kan inte stämma då a>0.
Vad är det jag missar?
Derivatan av F(a) är förvisso f(a) men derivatan av F(2a) är inte f(2a).
Tror inte jag förstår riktigt. Vad menar du?
Arean
T(a) = F(2a)-F(a)
T'(a)=F'(2a)*2-F'(a)=f(2a)*2-f(a)
Om du vill kan du prova den mer komplicerade vägen genom att räkna ut F(x) och se vad du får.
Precis. Det var det jag gjorde först. Men sen tänkte jag att om arean ändå ska deriveras kommer den primitiva funktionen också att deriveras och då kanske man på något sätt kan behålla ursprungsfunktionen. Vad menar Trinitity2 med att derivatan för F(2a) är F'(2a) * 2? Behöver man verkligen använda kedjeregeln?
Anonym_15 skrev:Precis. Det var det jag gjorde först. Men sen tänkte jag att om arean ändå ska deriveras kommer den primitiva funktionen också att deriveras och då kanske man på något sätt kan behålla ursprungsfunktionen. Vad menar Trinitity2 med att derivatan för F(2a) är F'(2a) * 2? Behöver man verkligen använda kedjeregeln?
Ja, F har en inre funktion 2a som man måste ta hänsyn till.
Anonym_15 skrev:[...]
Vad menar Trinitity2 med att derivatan för F(2a) är F'(2a) * 2? Behöver man verkligen använda kedjeregeln?
Din teori var att om F'(a) = f(a) så är F'(2a) = f(2a).
Det är jättebra att leta efter genvägar med hjälp av sådana teorier. Men om man inte är absolut säker på att teorin stämmer så bör man testa den.
I det här fallet kan du snabbt testa om teorin verkar stämma genom att prova med ett par olika enkla funktioner.
Provskott 1:
Om f(x) = x så är F(x) = x2/2+C.
Då är F(2x) = (2x,)2/2+C och alltså F'(2x) = 2*(2x)*2/2 = 4x, vilket inte är samma sak som f(2x) = 2x.
Provskott 2:
Om f(x) = ex så är F(x) = ex+C.
Då är F(2x) = e2x+C och alltså F'(2x) = e2x*2, vilket inte är samma sak som f(2x) = e2x.
=====
Slutsats: I inget av dessa fall gäller att F'(2x) = f(2x). Alltså kan inte detta samband gälla generellt.
Tack!



