Bestäm D om sin(x) och cos(x)+D ska möta varandra endast en gång per period

Jag skulle rita först.

Laguna skrev:

Jag skulle rita först.

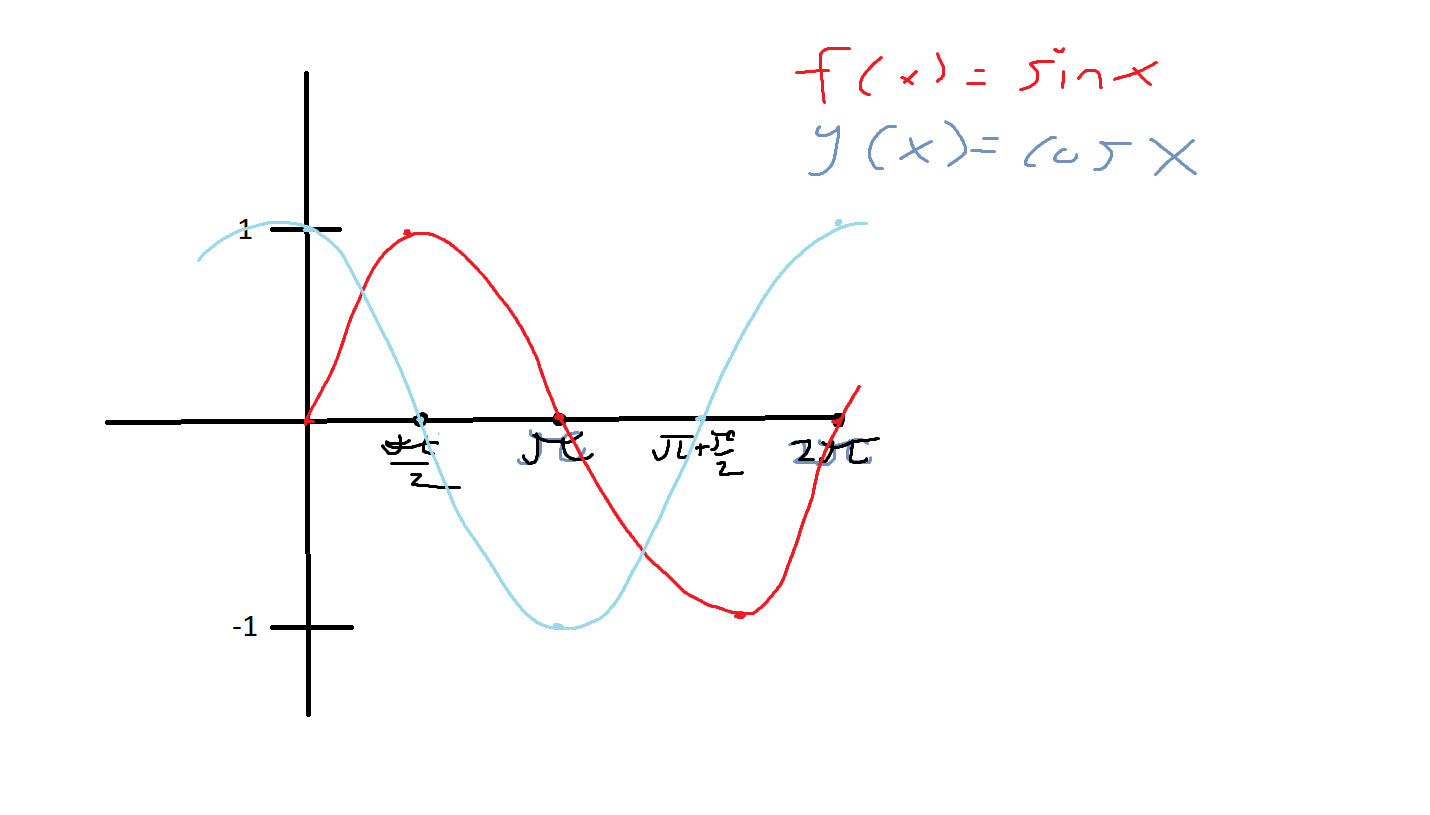Vi fick inte använda geogebra eller miniräknare, ungefår så här ritade jag ut det.

Snyggt. Man ser, tycker jag, att cos ligger mer än 1 under sin, som mest.

Hur stort är avståndet, som funktion av x? Hur hittar man dess största värde?

Laguna skrev:

Snyggt. Man ser, tycker jag, att cos ligger mer än 1 under sin, som mest.

Hur stort är avståndet, som funktion av x? Hur hittar man dess största värde?

Med d? eller utan?

Cos(x)-sin(x)
derivatan av cos(x)-sin(x) och sätter den lika med 0?

Sätta derivatan till 0, ja. Sedan räknar du ut vad detta största avstånd är.

Laguna skrev:

Sätta derivatan till 0, ja. Sedan räknar du ut vad detta största avstånd är.

Jag får fram att maximala avståndet är$\frac{1+\sqrt{3}}{2}$ . Är det korrekt? och hur fortsätter jag sedan?

Vad händer om du sätter D till det?

Laguna skrev:

Vad händer om du sätter D till det?

Nu har jag ju räknat cos - sin, så om jag subtraherar det från cos får jag sin?

alltså cos x - (avståndet) = sin x

men, hur vet jag att det inte kommer finnas några andra ställen där de skär?

Fanns det fler lösningar inom en period?

bbystrom skrev:

Laguna skrev:

Sätta derivatan till 0, ja. Sedan räknar du ut vad detta största avstånd är.

Jag får fram att maximala avståndet är$\frac{1+\sqrt{3}}{2}$ . Är det korrekt? och hur fortsätter jag sedan?

det har var fel förresten, det blev sqrt(2) och det finns bara en lösning. 

Ser du hur det ser ut då när du ritar både sin(x) och cos(x)+sqrt(2)?

Laguna skrev:

Ser du hur det ser ut då när du ritar både sin(x) och cos(x)+sqrt(2)?

Ja.

Laguna skrev:

Ser du hur det ser ut då när du ritar både sin(x) och cos(x)+sqrt(2)?

Men jag har fortfarande svårt att vira huvudet runt varför man bara kan använda max avståndet som D..

En variant är att skriva om ekvationen som 

$D=\sin x - \cos x = 1 \cdot \sin x + (-1)\cdot \cos x$

Använd att

$a\sin x +b \cos x =\sqrt{a^2+b^2}\sin(x+v)$

där 

$\tan v=\dfrac{b}{a}$

För vilka värden på D har

$D=\sqrt{2}\sin(x-\frac{\pi}{4})$

endast en lösning per period?