Bestäm bild (linjära avbildningar)

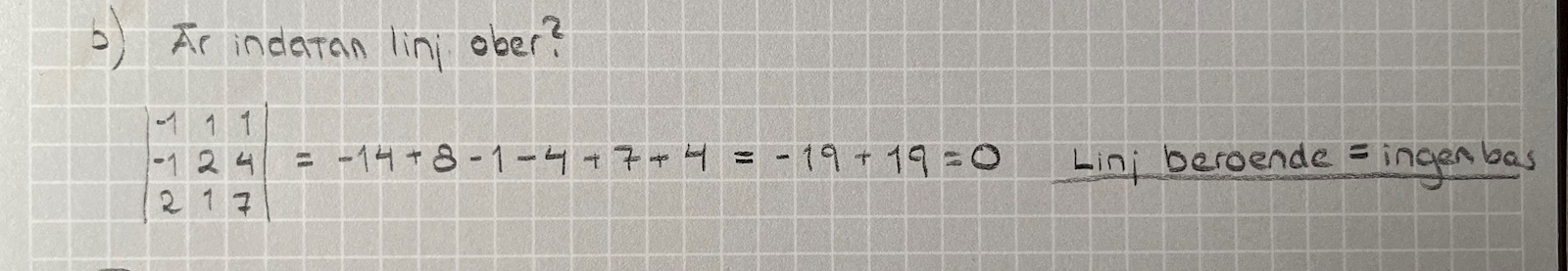
Kan du några regler för linjära avbildningar? Hur ligger det till med definitionen? Vad gäller t.ex. för

$F(\lambda\left(\mathbf{u}+\mathbf{v}\right))=?$

D4NIEL skrev:

Kan du några regler för linjära avbildningar? Hur ligger det till med definitionen? Vad gäller t.ex. för

$F(\lambda\left(\mathbf{u}+\mathbf{v}\right))=?$

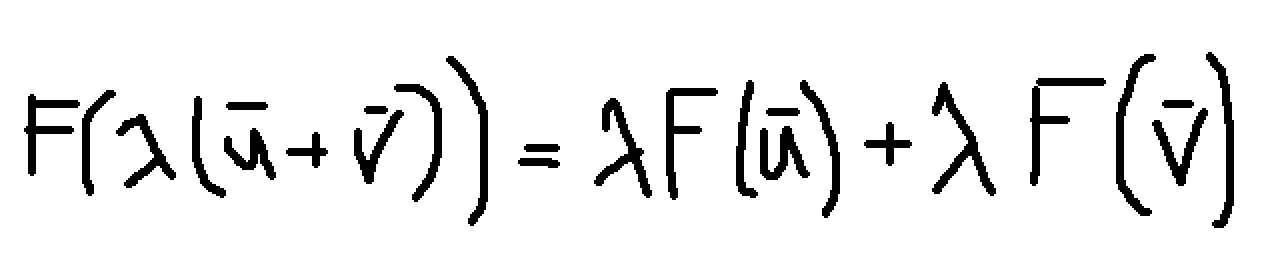
Tänker att man kan skriva om det så här, men vet inte riktigt hur det ska hjälpa mig i denna uppgift

Om du sätter $\lambda_1=1$ samt $u=(-1,-1,2)$ och $v=(1,2,1)$ så blir

$F(u+v)=F(0,1,3)=F(-1,-1,2)+F(1,2,1)$

Är du med?

På b) kan du bevisa att (0,1,2) är linjärt oberoende av de övriga genom att visa att determinanten är nollskild (full matrisrank)

D4NIEL skrev:

Om du sätter $\lambda_1=1$ samt $u=(-1,-1,2)$ och $v=(1,2,1)$ så blir

$F(u+v)=F(0,1,3)=F(-1,-1,2)+F(1,2,1)$

Är du med?

På b) kan du bevisa att (0,1,2) är linjärt oberoende av de övriga genom att visa att determinanten är nollskild (full matrisrank)

Jag är med på att det du skriver stämmer regelmässigt, men jag är fortfarande osäker på varför jag gör det. Hur kommer det sig att vi plockar ut just dessa vektorer u och v? Och varför bara två vektorer, när vi arbetar i R3? Och hur kommer jag vidare efter den ekvation du nu ställt upp? Ber om ursäkt för många frågor, men vill verkligen förstå detta!

Edit: Nu förstår jag tror jag! Men, min fundering nu är snarare då om denna uppgift enbart går att lösa tack vare att vi "enkelt" kunde se att (-1, -1, 2) + (1, 2, 1) = (0, 1, 3) och att vi faktiskt hade just de vektorerna u och v i vår uppgift? För låt säga vi inte visste vad F(-1,-1,2) var lika med, då hade väl uppgiften varit omöjlig att lösa? Tack för hjälpen alla fall!

På b) uppgiften har du just den situation jag tror att du undrar över. Det kommer visa sig omöjligt att teckna $(0,1,2)$ som en linjärkombination av (spannet av) vektorerna du får i 11b

Det kan du visa genom att ställa upp ekvationen (linjärkombinationen)

$\lambda_1(-1,-1,2)+\lambda_2(1,2,1)+\lambda_3(1,4,7)=(0,1,2)$

Om det inte finns några $\lambda_i$ som uppfyller ekvationen kan du inte uttrycka $(0,1,2)$ som en linjärkombination av de tillgängliga vektorerna.

D4NIEL skrev:

På b) uppgiften har du just den situation jag tror att du undrar över. Det kommer visa sig omöjligt att teckna $(0,1,2)$ som en linjärkombination av (spannet av) vektorerna du får i 11b

Det kan du visa genom att ställa upp ekvationen (linjärkombinationen)

$\lambda_1(-1,-1,2)+\lambda_2(1,2,1)+\lambda_3(1,4,7)=(0,1,2)$

Om det inte finns några $\lambda_i$ som uppfyller ekvationen kan du inte uttrycka $(0,1,2)$ som en linjärkombination av de tillgängliga vektorerna.

Stort tack för hjälpen! Så en linjärkombination är också en form av linjär avbildning? :)

Mja, jag tror du menar rätt, men vi måste vara försiktiga med formuleringen. Klart är att om du känner till några vektorer t.ex.

$F(u)$, $F(v)$ och $F(w)$ så känner du också till alla linjärkombinationer av dem t.ex.

$F(3u+2v)$ eller $F(5v-3w)$

Om u,v och w är linjärt oberoende i $\mathbb{R}^3$ så kan du alltså nå hela rummet och därmed återskapa avbildningsmatrisen.

En linjär avbildning av en linjär avbildning kallas komposition och är förvisso också linjär, men ligger kanske lite utanför ramen för inledande linjär algebra. Man kan visa att kompositionens matris är produkten av de två linjära avbildningsmatriserna.