bestäm avstånd

har kommit fram till
1,0²=1.2²+x²-2*1.2*x*cos30
men efteråt så går jag vilse eftersom jag får fel svar hela tiden! förstår verkligen inte hur man löser ut x, har testat allt från faktorisering till pq formeln.
rätt svar är 0,24m och 1,84m
Hej!
Du har gjort helt rätt, och har försökt med rätt metoder. Bra!
Vi skriver om din ekvation så den ser ut som andragradsfunktion på standardform först, alltså
Vi kan lösa den algebraiskt, vilket kräver väldigt mycket mer arbete än att lösa med hjälp av t.ex. miniräknare, desmos eller GeoGebra!
Ekvationen vi vill lösa är alltså
Sätter vi in i Desmos och klicka på nollställena får vi:
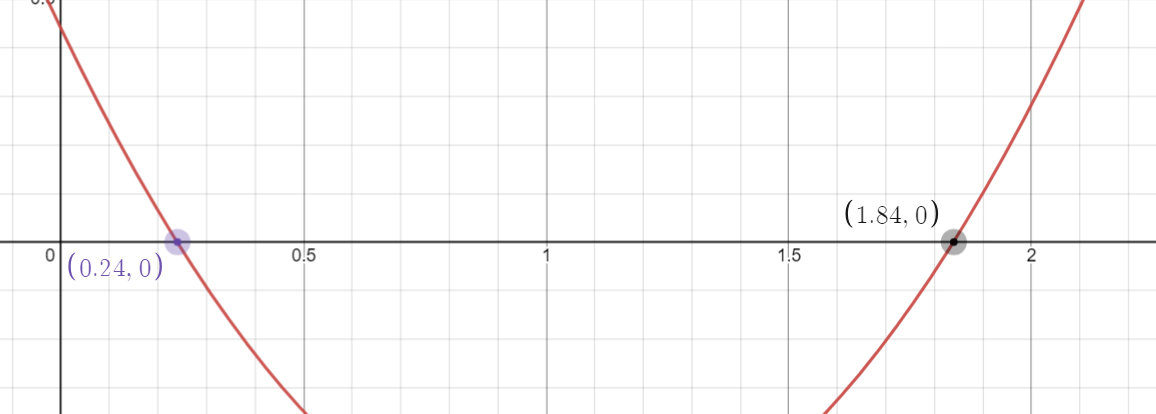
puss på dig men tyvärr måste det vara en algebraisk lösning
Med pq får vi
Lösningarna blir alltså:
fattar dock inte hur du kom fram till roten ur tre?
här är fel svar men den lösningen jag använde:
1,0²=1.2²+x²-2*1.2*x*cos30
1=1,44+x²-2.07...x
0=x²-2.07...x+0,44
x=2.07.../2 +- (roten ur: (2.07/2)²-0.44)
x=2.07.../2 +- 0.8
oj vänta nu råkade jag lösa den.
fast kan du fortfarande berätta vart roten ur tre kom från?
Roten ur 3 kommer från att
(Finns i formelbladet :D)
just ja hahaha tack så mkt


