Skriv de komplexa talen på polär form och försök att utnyttja att Arg (z/w) = Arg z - Arg w.
Jag skrev ihop 1 i nämnaren med det övriga och multiplicerade täljaren med nämnaren där till att börja med. Leder det någonstans.

Jag förstår det du skrev först.
Det bråket kan förenklas till 1+i√31+i
Men jag förstår inte vad du skriver på raden under.
Okej, då ska man inte göra så då. Tänkte som vid division om man ska dividera 8/2 sedan med 2 igen, så kan man lika gärna multiplicera ihop 2orna för samma resultat.
Men jag multiplicerar med konjugatet till 1+i istället för det står att man ska göra det i en tidigare uppgift.
Då får man följande resultat..
Och jag måste tillägga att uppgiften är alldeles för svår för mig, jag förstår i princip inte ens vad det står egentligen.

Du behöver inte förlänga med konjugatet.
Uttrycket du ska ta fram argumentet för är z1z2z3, där z1=i, z2=1+i√3 och z3=1+i.
Kommer du vidare med tipset jag gav i svar #2?
Lite kanske.

Du behöver inte skriva ut alla tal. Det räcker att ta reda på argumentet för respektive tal.
Börja då med att markera de tre talen i det komplexa talplanet.
Visa din bild.
Förstår inte vad du menar med att det inte behövs skrivas ut tal.
Eller du menar Z1 = π/2 z3 = π/4 och Z2 = Tan(√3/1) (vad nu det är)?
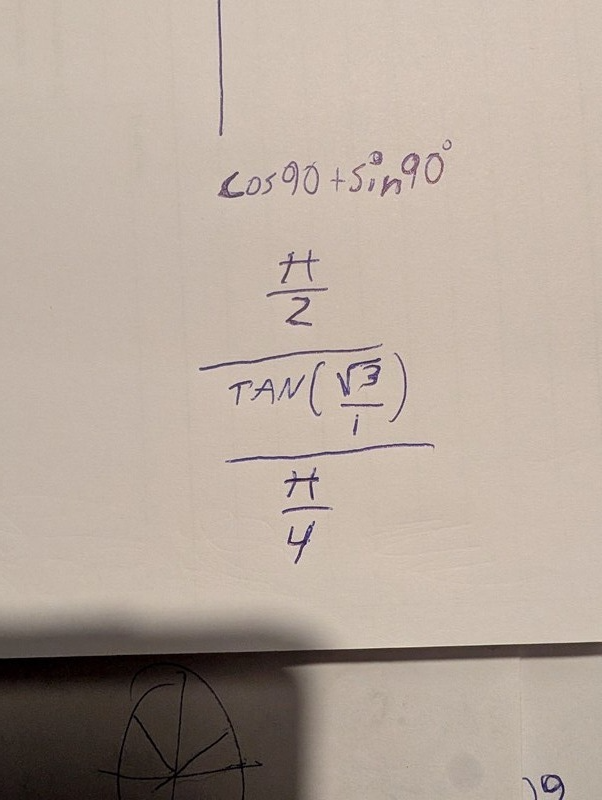

Dkcre skrev:Förstår inte vad du menar med att det inte behövs skrivas ut tal.
Enligt räkneregeln i svar #2 så är Arg (z1/(z2/z3)) = Arg z1 - (Arg z2 - Arg z3)
Eller du menar Z1 = π/2 z3 = π/4 och Z2 = Tan(√3/1) (vad nu det är)
Ja nästan.
Det gäller att Arg z1 = pi/2, Arg z3 = pi/4 och att Arg z2 = arctan(√3) (vilket är en känd vinkel).
Läs gärna mer om detta här.
Jo arctan blir det ja.
Så π/2 - π/3 - π/4
6π/12-4π/12-3π/12 = -π/12
Eller så blir det 5π/12 kanske
Enormt svårt .
Tack för hjälpen..
Dkcre skrev:Jo arctan blir det ja.
Så π/2 - π/3 - π/4
Nej, det blir pi/2-(pi/3-pi/4)
6π/12-4π/12-3π/12 = -π/12
Eller så blir det 5π/12 kanske
Ja, 5pi/12 är rätt
Enormt svårt .
Som med så mycket annat så är det svårt i början, men det blir lättare efter ett antal uppgifter.




