Bestäm arean för BCEF (Matematik/Matte 2/Logik och geometri)

Arup skrev:
En parallellogram ABCD har sidorna AB = 2 och AD = 3. Vinkeln A är60◦. Låt E vara mittpunkten på CD och låt F vara skärningspunkten försträckorna BD och AE. Bestäm arean för fyrhörningen BCEF.

Som vanligt: Börja med att rita. Lägg upp din bild här.

ok, jag gör det på eftermiddag

Arup skrev:
En parallellogram ABCD har sidorna AB = 2 och AD = 3. Vinkeln A är60◦. Låt E vara mittpunkten på CD och låt F vara skärningspunkten försträckorna BD och AE. Bestäm arean för fyrhörningen BCEF.

Kan analytisk geometri användas?

jag tror det

Arup skrev:
jag tror det

Den blir betydligt enklare då, men kanske någon vill lösa den på klassiskt sätt först?

Trinity2 skrev:
Arup skrev:
jag tror det

Den blir betydligt enklare då, men kanske någon vill lösa den på klassiskt sätt först?

spelar det någon roll ?

Trinity2 skrev:
Arup skrev:
En parallellogram ABCD har sidorna AB = 2 och AD = 3. Vinkeln A är60◦. Låt E vara mittpunkten på CD och låt F vara skärningspunkten försträckorna BD och AE. Bestäm arean för fyrhörningen BCEF.

Kan analytisk geometri användas?

Vad menar du med analytisk geometri? Tråden ligger i Ma2.

aha jag tolkade det som att avstånds och mittpunkts formeln skulle användas. Då har väl Trinity fel ?

Smaragdalena skrev:
Trinity2 skrev:
Arup skrev:
En parallellogram ABCD har sidorna AB = 2 och AD = 3. Vinkeln A är60◦. Låt E vara mittpunkten på CD och låt F vara skärningspunkten försträckorna BD och AE. Bestäm arean för fyrhörningen BCEF.

Kan analytisk geometri användas?

Vad menar du med analytisk geometri? Tråden ligger i Ma2.

Jag utgår från att man vet vad ett koordinatsystem och en rät linje är i Ma2. Uppgiften blir trivial då.

(Att något ligger på XYZ betyder, har jag fått erfara, litet, då uppgifter postas hej vilt på olika ställen med olika förutsättningar.)

Trinity2 skrev:
Smaragdalena skrev:
Trinity2 skrev:
Arup skrev:
En parallellogram ABCD har sidorna AB = 2 och AD = 3. Vinkeln A är60◦. Låt E vara mittpunkten på CD och låt F vara skärningspunkten försträckorna BD och AE. Bestäm arean för fyrhörningen BCEF.

Kan analytisk geometri användas?

Vad menar du med analytisk geometri? Tråden ligger i Ma2.

Jag utgår från att man vet vad ett koordinatsystem och en rät linje är i Ma2. Uppgiften blir trivial då.

(Att något ligger på XYZ betyder, har jag fått erfara, litet, då uppgifter postas hej vilt på olika ställen med olika förutsättningar.)

Du har fortfarande inte förklarat vad du menar med "analytisk geometri".

Smaragdalena skrev:
Trinity2 skrev:
Smaragdalena skrev:
Trinity2 skrev:
Arup skrev:
En parallellogram ABCD har sidorna AB = 2 och AD = 3. Vinkeln A är60◦. Låt E vara mittpunkten på CD och låt F vara skärningspunkten försträckorna BD och AE. Bestäm arean för fyrhörningen BCEF.

Kan analytisk geometri användas?

Vad menar du med analytisk geometri? Tråden ligger i Ma2.

Jag utgår från att man vet vad ett koordinatsystem och en rät linje är i Ma2. Uppgiften blir trivial då.

(Att något ligger på XYZ betyder, har jag fått erfara, litet, då uppgifter postas hej vilt på olika ställen med olika förutsättningar.)

Du har fortfarande inte förklarat vad du menar med "analytisk geometri".

Min hemmagjorda terminologi på allt som ej förekommer i Elementa.

Då är det inte så konstigt att jag inte vet vad du menar - det låter väldigt avancerat! Det är mycket möjligt att du menar något som hör till Ma2, men jag vet inte.

Smaragdalena skrev:
Då är det inte så konstigt att jag inte vet vad du menar - det låter väldigt avancerat! Det är mycket möjligt att du menar något som hör till Ma2, men jag vet inte.

Kanske någon kan lösa denna uppgift med en "magisk linje" som oftast brukar vara fallet med geometriuppgifter. Uppgiften är inte svår om man använder hela "verktygslådan", men jag tror denna uppgift blir vackrare ju färre 'verktyg' man använder. Kanske någon volontär har ett bra angreppssätt.

Någonting i denna stil, men jag tror det finns en bättre 'Elementa-lösning';

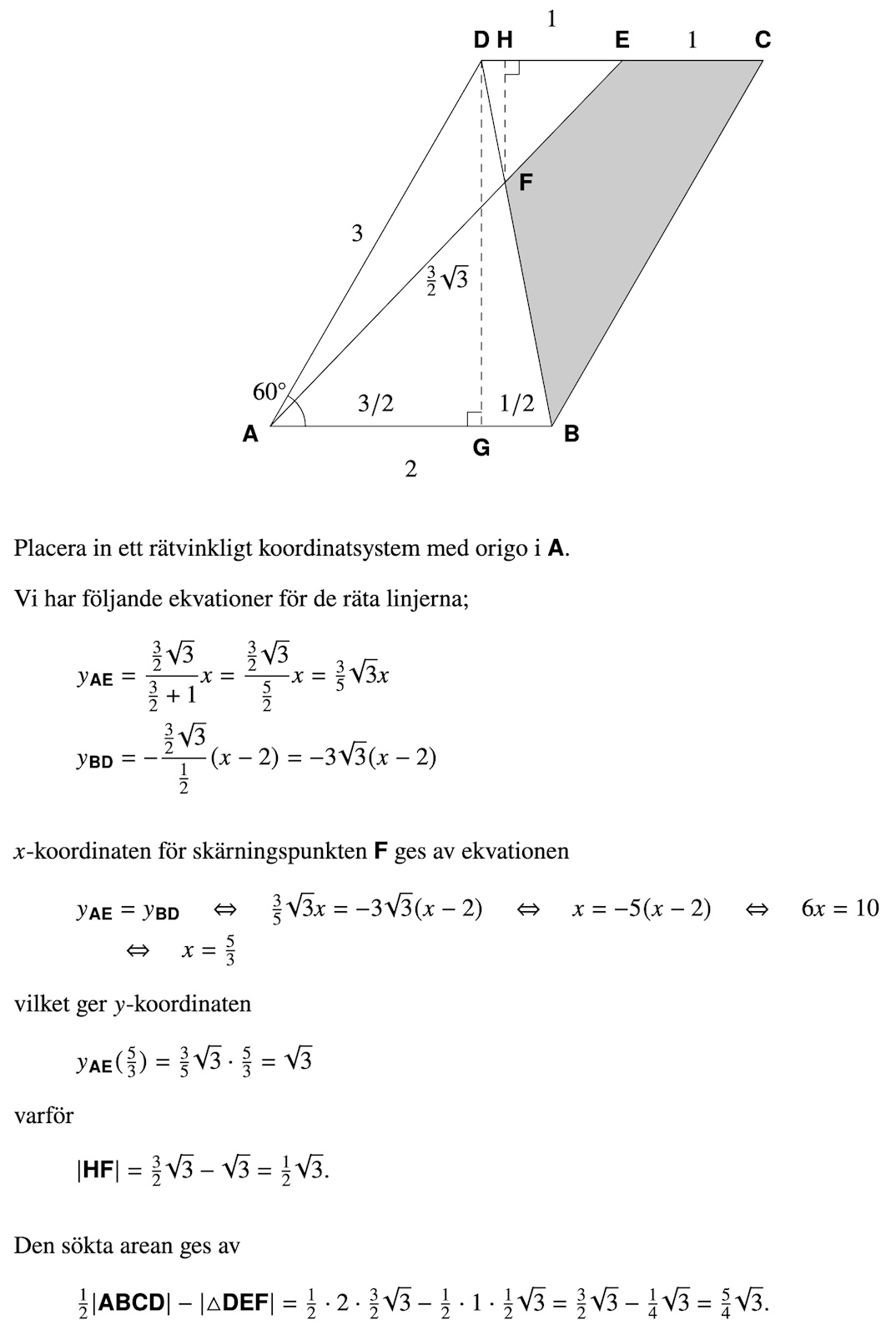
Att HF = $\sqrt{3} / 2$ ges väl direkt av att trianglarna DFE och ABF är likformiga.

Louis skrev:
Att HF = $\sqrt{3} / 2$ ges väl direkt av att trianglarna DFE och ABF är likformiga.

hur vet vi att de är likformiga ?

Louis skrev:
Att HF = $\sqrt{3} / 2$ ges väl direkt av att trianglarna DFE och ABF är likformiga.

Så är det nog. Synd inte bra kommentarer kommer tidigare. Tror jag skall sätta lösningar i 2 månaders karantän. De mår de säkert bra av.

Smaragdalena skrev:
Då är det inte så konstigt att jag inte vet vad du menar - det låter väldigt avancerat! Det är mycket möjligt att du menar något som hör till Ma2, men jag vet inte.

För mig betyder analytisk geometri att man använder ett koordinatsystem. Det som Descartes införde.

hur vet vi att de är likformiga ?

Vinklarna är lika (alternatvinklar vid parallella linjer).

Louis skrev:

hur vet vi att de är likformiga ?

Vinklarna är lika (alternatvinklar vid parallella linjer).

Vilken är den 'optimala' lösningen?

Parallellogrammens höjd är $\frac{3}{2} \sqrt{3}$ .
Den sträckan är summan av de likformiga trianglarnas höjder.

Då DE:AB = 1:2 är även förhållandet mellan höjderna 1:2 och HF/DG = 1/3.
HF = $\sqrt{3} / 2$ .
A_DFE = $\frac{1}{2} \times 1 \times \sqrt{3} / 2 = \sqrt{3} / 4$ .

Triangel DBC har dubbel bas och 3 gånger så lång höjd och är alltså 6 gånger så stor,
vilket ger det sökta området 5 gånger så stort.
A_BCEF = $\frac{5}{4} \sqrt{3}$ .

Louis skrev:
Parallellogrammens höjd är $\frac{3}{2} \sqrt{3}$ .
Den sträckan är summan av de likformiga trianglarnas höjder.

Då DE:AB = 1:2 är även förhållandet mellan höjderna 1:2 och HF/DG = 1/3.
HF = $\sqrt{3} / 2$ .
A_DFE = $\frac{1}{2} \times 1 \times \sqrt{3} / 2 = \sqrt{3} / 4$ .

Triangel DBC har dubbel bas och 3 gånger så lång höjd och är alltså 6 gånger så stor,
vilket ger det sökta området 5 gånger så stort.
A_BCEF = $\frac{5}{4} \sqrt{3}$ .

Louis den här är nog mer tjusig än Trinity:s lösning