bestäm area
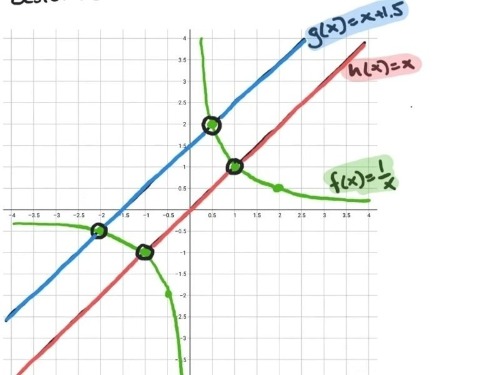
Hur bestämmer man vilken som är övre respektive undre funktionen vid sådana fall för att bestämma området i mitten? Och hur långt vet man de sträcker sig? (övre och undre integrationsgräns) Fattar inte hur man gör här och hur man kan tänka allmänt.
Rätt uppställning:
Dela upp området i mindre delar.
I skärningspunkterna kommer det bli gränser. Sätt funktionerna lika med varandra för att beräkna skärningspunkterna.
mrpotatohead skrev:Dela upp området i mindre delar.
I skärningspunkterna kommer det bli gränser. Sätt funktionerna lika med varandra för att beräkna skärningspunkterna.
Ja jag är med på att de ska delas upp i mindre delar och att skärningspunkterna skapar gränser. Men inte hur man går tillväga.
Så hät:
- Du får fram x1 och x3 genom att lösa ekvationen f(x) = g(x).
- Du får fram x2 och x4 genom att lösa ekvationen f(x) = h(x)
- Du får fram arean av omrpde A genom att integrera g(x)-f(x) från x1 till x2
- Du får fram arean av område B genom att integrera g(x)-h(x) från x2 till x3
- Du får fram arean av område C genom att integrera f(x)-h(x) från x3 till x4
- Det som efterfrågas är sedan summan av dessa tre areor

Fråga gärna om du vill ha mer förtydligande.
Tack för förtydligandet!
Men verkar inte förstå hur man kommer fram till detta
- Du får fram arean av omrpde A genom att integrera g(x)-f(x) från x1 till x2
- Du får fram arean av område B genom att integrera g(x)-h(x) från x2 till x3
- Du får fram arean av område C genom att integrera f(x)-h(x) från x3 till x4
När jag ser det på bilden verkar det helt klart.
Men jag förstår inte hur man ska tänka och veta vilka man man ska integrera och subtrahera med varandra? Hur vet jag vart gränserna går?
Tillägg: 3 nov 2023 12:59
Varför kan man exempelvis inte bara räkna ut område b som en hel integral mellan g(x)-h(x) med gränserna -1 och 1?
naturnatur1 skrev:[...]
Men jag förstår inte hur man ska tänka och veta vilka man man ska integrera och subtrahera med varandra? Hur vet jag vart gränserna går?
Det ör en förmåga som går att träna upp. Öva på att dela upp området i olika intervall med hjälp av vertikala linjer på ett sådant sätt att det I varje intervall endast är två funktioner inblandade: En "övre" och en "undre" funktion, se bild:

Tillägg: 3 nov 2023 12:59
Varför kan man exempelvis inte bara räkna ut område b som en hel integral mellan g(x)-h(x) med gränserna -1 och 1?
Eftersom du då skulle få fram arean av det streckade området i följande bild.

Du måste istället tönka vertikala linjer som uppdelare/avgränsare enligt det jag skrev ovan.



