Bestäm antal punkter
Fattar inte riktigt frågan 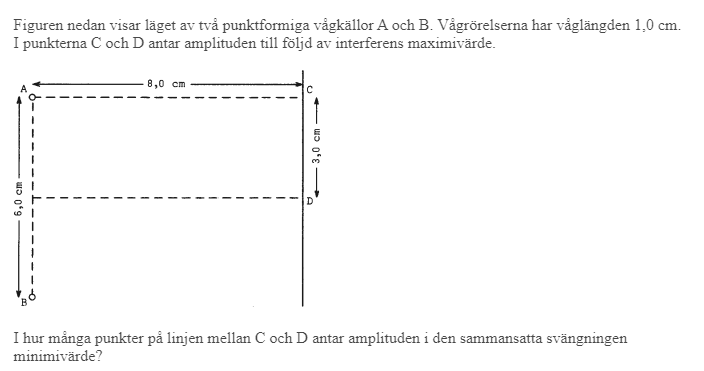
Bayan Ali skrev:Fattar inte riktigt frågan
Frågan är hur många nodlinjer det ligger mellan C och D.
Okej, då måste det väl vara 3st
våglängden är 1 cm och vi har 3cm därmed 3lambda
så det måste finnas en nodlinje vid 0,5; 1,5 och 2,5lambda
Bayan Ali skrev:Okej, då måste det väl vara 3st
våglängden är 1 cm och vi har 3cm därmed 3lambda
så det måste finnas en nodlinje vid 0,5; 1,5 och 2,5lambda
Avståndet mellan nodlinjer är inte lika med våglängden.
Okej, men hur är det man kan bestämma antalet nodlinjer
Vad är skillnaden i väg mellan A-C och B-C? Hur många våglängder blir det?
2cm -> 2 våglängder
Hur många interferensmaxima får vi då på linjen mellan C och D?
Vi har inte gått igenom "interferensmaxima", jag vet inte vad det är. Finns det ett annat namn på den?
Hoppsan, jag använder kanske inte rätt uttryck. Vad jag menar är att uppgiften ger oss att vi får max amplitud genom interferens i punkterna C och D. D.v.s skillnaden i gångväg är ett helt antal våglängder. För A-D och B-D är skillnaden noll, för A-C och B-C är skillnaden 2 våglängder.
Finns det då någon punkt mellan C och D där vi får 1 våglängd i skillnad?
Ja, mellan de, avståndet 1,5cm från varje
Bayan Ali skrev:avståndet 1,5cm från varje
Nej (men det exakta stället spelar ingen roll).
Det är maxima i C, D och ett mittemellan. Var finns då minima? Eller viktigare, hur många?
2 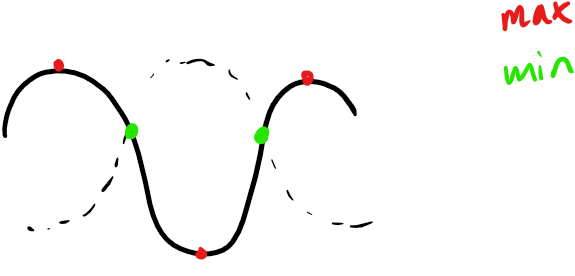
Tänker jag rätt?
Bayan Ali skrev:2
Tänker jag rätt?
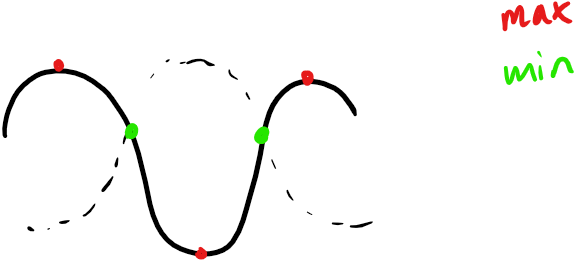
Om jag tolkar din bild rätt: Nej. Vid den röda punkten är den ena kurvan maximalt negativ och den andra maximalt positiv, så summan blir 0.
Eftersom du inte skriver särskilt tydligt vad din bild föreställer, är det fullt möjlig tatt jag tolkar den alldeles fel.
Jag tänker att de röda uppe är C och D och den röda nere är maximi punkten mellan de. De gröna är därför minimipunkterna
Menar du att vågorna varierar jättemycket vid de röda punkterna, och att de gröna punkterna ligger stilla? I så fall har du rätt.
Aa jag tänkte så, men jag var osäker då jag har ritat 1,5lambda och det ska egentligen vara 3lambda
Jag har en liten figur jag använt förr som ska förklarar fenomenet interferens. Varför vågorna ibland släcker ut varandra (minima) och ibland förstärker varandra (maxima):

Sträckan är skillnaden i gångväg till punkten P. Sträckan s är samma för båda.
Δs är 4 våglängder och därmed är det maxima i det här fallet, ellerhur
Nej, det är nog 4.5 våglängder och det blir ett minima i punkten P.
Aa ser det nu