Bestäm alla x för vilka serien konvergerar

Uppgiften lyder:

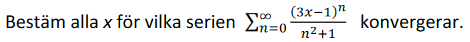
och jag är lite osäker hur jag ska resonera...

Räcker det att tänka såhär?

$= \sum_{n = 0}^{\infty} (\frac{3^{n}}{n^{2} + 1}) {(x - \frac{1}{3})}^{n} d ä r a_{n} = \frac{3^{n}}{n^{2} + 1} o c h r = (x - \frac{1}{3})$

och att enligt detta sambandet

$\sum_{n = 0}^{\infty} a r^{n} \Rightarrow k o n v e r g e r a r o m |r| < 1$

landa i att

$|x - \frac{1}{3}| < 1 \Rightarrow 0 \leq x \leq \frac{2}{3}$

Hur gör man för att veta att det ska vara $\leq$ och inte < ? Tänker man såhär över huvud taget?

Hur kommer du fram till implikationen som står efter "landa i att"?

Vänsterledet implicerar att kan x ligga i (-2/3, 4/3).

Laguna skrev:
Hur kommer du fram till implikationen som står efter "landa i att"?

Vänsterledet implicerar att kan x ligga i (-2/3, 4/3).

Hmmm... tror att denna lösning kanske stämmer i sitt resonemang?

Jag tror det blir bäst om du inte bryter ut 3 från 3x-1, utan behandlar (3x-1)ⁿ hela tiden.

Steg 1 och 2 ser rätt ut, även om det blir lite mycket räknande fram och tillbaka. Steg 3 vet jag inte vad du gör, känns inte som att uträkningen håller även om svaret råkar stämma.

Micimacko skrev:
Steg 1 och 2 ser rätt ut, även om det blir lite mycket räknande fram och tillbaka. Steg 3 vet jag inte vad du gör, känns inte som att uträkningen håller även om svaret råkar stämma.

Tänkte att jag kan använda $\sum_{n = 1}^{\infty} a r^{n} |r| < 1 \Rightarrow k o n v e r g e n t$

Hur gör man annars för att testa endpunkterna?

Problemet är att ditt a går mot oändligheten. Jag vet inte exakt vilka krav det ska vara på a, begränsad borde räcka, men här kan du inte använda det. Stoppa in ändpunkterna och se vad du får för serie till att börja med.

Micimacko skrev:
Problemet är att ditt a går mot oändligheten. Jag vet inte exakt vilka krav det ska vara på a, begränsad borde räcka, men här kan du inte använda det. Stoppa in ändpunkterna och se vad du får för serie till att börja med.

Det är det jag gjorde i steg 3, och jag ser serien som en geometrisk serie som då är konvergent om absolutbeloppet av r är mindre än 1 vilket det blir för båda ändpunkterna, eller kan man inte se serien som en geometrisk serie?

Nej, man kan bara se serien som en geometrisk serie om det är en geometrisk serie. Vad får du om du stoppar in tex x=0? Ser den konvergent eller divergent ut?

Micimacko skrev:
Nej, man kan bara se serien som en geometrisk serie om det är en geometrisk serie. Vad får du om du stoppar in tex x=0? Ser den konvergent eller divergent ut?

Kan man resonera såhär?

För x=0 gäller

$\sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{n^{2} + 1} k o n v e r g e n t f ö r d e n ä r a l t e r n e r a n d e o c h f ö l j d e n \frac{1}{n^{2} + 1} = 0 d å n \to \infty$

För x=2/3 gäller

$\sum_{n = 0}^{\infty} \frac{1^{n}}{n^{2} + 1} k o n v e r g e n t f ö r \frac{1}{n^{2} + 1} = 0 d å n \to \infty$

För x=2/3 behövs det mer. Summan av 1/n är t.ex. inte konvergent trots att termerna går mot 0.

Svara Avbryt

Visa senaste svar