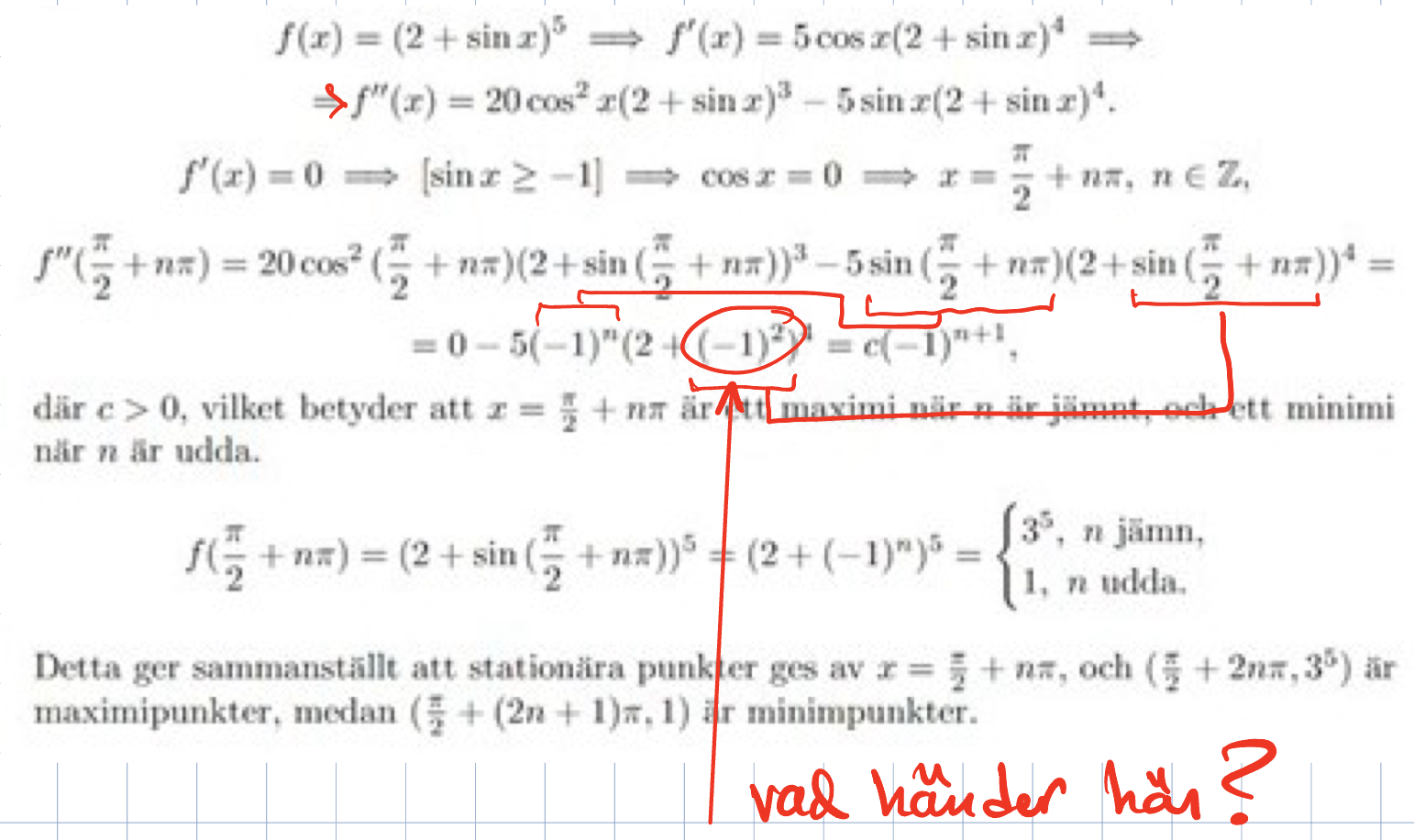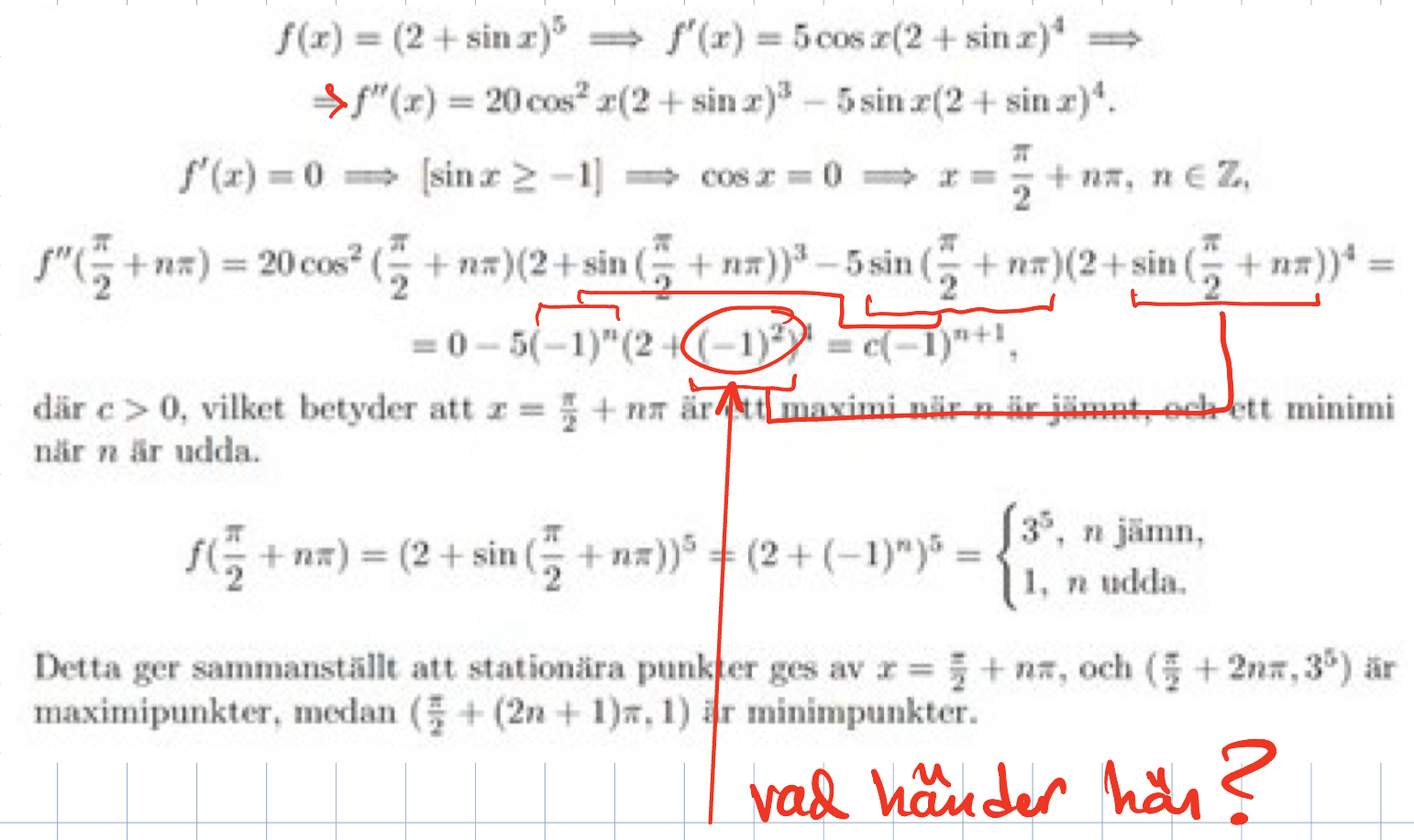Bestäm alla stationära punkter och deras karaktärer.
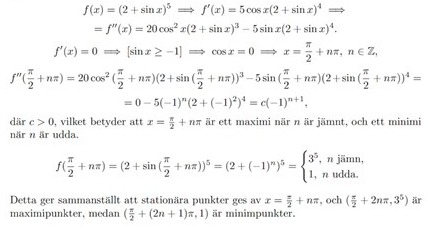
Har lite svårt att förstå denna uppgiften. Jag förstår det algebraiska ända fram tills han säger att sinx>-1. Varför? Hur?
Och varför görs det ett allmänt uttryck för andraderivatan? Varför t.ex. inte enbart räkna på och -?
Den trigonometriska funktionen sin(x) har en begränsad värdemängd. Den kan aldrig avbilda ett värde utanför intervallet [-1,1]. DVS sin(x) är begränsad inom intervallet: -1 ≤ sin x ≤ 1. Detta kan tolkas geometrisk som att en katet aldrig kan vara större än hypotenusan i en rätvinklig triangel.
Anledningen till att det görs ett allmänt uttryck för andraderivatan är för att man även behöver bestämma de stationära punkternas karaktär, alltså om det är en lokal maximi- eller minimipunkt.
Trinity2 skrev:
Väldigt bra fråga. Ingen aning faktiskt. Sin pi/2 är väl 1? Och varför upphöjt till n?
Truppeduppe skrev:Den trigonometriska funktionen sin(x) har en begränsad värdemängd. Den kan aldrig avbilda ett värde utanför intervallet [-1,1]. DVS sin(x) är begränsad inom intervallet: -1 ≤ sin x ≤ 1. Detta kan tolkas geometrisk som att en katet aldrig kan vara större än hypotenusan i en rätvinklig triangel.
Anledningen till att det görs ett allmänt uttryck för andraderivatan är för att man även behöver bestämma de stationära punkternas karaktär, alltså om det är en lokal maximi- eller minimipunkt.
Men ansattes inte precis sinx=-1 i derivatan? För annars hade väl inte cosx blivit noll? Varför just -1 när det är ett intervall?
När de sätter f'(x)=0 använder de nollproduktsmetoden, dvs om en produkt är lika med 0 måste minst någon av de ingående faktorerna vara lika med 0. Eftersom att 5 inte är 0 och 2-sin(x) inte är 0 (eftersom att sin(x)>=-1) måste faktorn cos(x) vara lika med 0. Från detta kan vi bestämma de stationära punkterna.
Därefter sätter man in de stationära punkterna i f''(x) för att bestämma om det är en maximi-eller mininipunkt. Notera att vi enbart behöver veta tecknet på f''(x), alla konstanter bakas in i c.
Calle_K skrev:När de sätter f'(x)=0 använder de nollproduktsmetoden, dvs om en produkt är lika med 0 måste minst någon av de ingående faktorerna vara lika med 0. Eftersom att 5 inte är 0 och 2-sin(x) inte är 0 (eftersom att sin(x)>=-1) måste faktorn cos(x) vara lika med 0. Från detta kan vi bestämma de stationära punkterna.
Därefter sätter man in de stationära punkterna i f''(x) för att bestämma om det är en maximi-eller mininipunkt. Notera att vi enbart behöver veta tecknet på f''(x), alla konstanter bakas in i c.
Tack!! Nu förstår jag.