Bestäm alla lokal extrempunkter inom en kompakt område



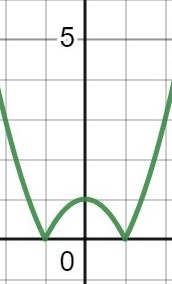
Det har uppstått lite problem när ja försöker skissa grafen till den här funktion inom kompakt intervallet -2 och 2.
Alltså det verkar som -1 ska vara en min punkt men när ja sätt in -1 in i f(x).
abs(-1-1)=2 men då blir f(-1) > f(0) vilken är inte rimligt.
Kan ni hjälp mig hittar var någonstans ja har gjort fel?
Marcus N skrev:
Det har uppstått lite problem när ja försöker skissa grafen till den här funktion inom kompakt intervallet -2 och 2.
Alltså det verkar som -1 ska vara en min punkt men när ja sätt in -1 in i f(x).
abs(-1-1)=2 men då blir f(-1) > f(0) vilken är inte rimligt.
Kan ni hjälp mig hittar var någonstans ja har gjort fel?
Vilket värde har (-1)2?
(-1)^2 =1
But funktions värde f(-1)=abs(-1-1)=2
Marcus N skrev:But funktions värde f(-1)=abs(-1-1)=2
Nej, (-1)2-1 = 0
Fast på några ställen har du (felaktigt) skrivit att f(x) = |x-1|, och DEN funktionen skulle ha f(-1) = 2:

Jag blev också förvirrad, på pappret har du högst upp skrivit abs(x-1), men i övrigt har du skrivit och räknat med abs (x^2-1)
En liten mini-kommentar på lösningen: du har skrivit f’(x) = två olika fall, sedan under det har det skrivit att f’(x) är odefinierad för x=-2, -1 osv. Men på raden över har du inkluderat dessa i intervallet för när derivatan är 2x. Det är ju motsägelsefullt.
För det stämmer att derivatan är odefinierad för dessa x, så du bör sätta () runt intervallen istället för []
Ja, för att derivatan för ej def. på någon ändpunkten då ska dem inte vara med.
Hondel skrev:Jag blev också förvirrad, på pappret har du högst upp skrivit abs(x-1), men i övrigt har du skrivit och räknat med abs (x^2-1)
Nej, uppgiften är f(x)=abs(x-1) inte abs(x^2-1).
Jag har ingen aning varför den andra volontärer vill beräkna (-1)^2 hela tiden.
Smaragdalena skrev:Marcus N skrev:But funktions värde f(-1)=abs(-1-1)=2
Nej, (-1)2-1 = 0
Fast på några ställen har du (felaktigt) skrivit att f(x) = |x-1|, och DEN funktionen skulle ha f(-1) = 2:
Varför vill du beräkna (-1)^2-1 hela tiden??
f(x) ska vara abs(x-1)!
Varför vill du beräkna (-1)^2-1 hela tiden??
f(x) ska vara abs(x-1)!
I så fall är praktiskt taget allt du skriver i ditt förstainlägg fel, eftersom den funktion som det handlar om där är f(x) = |x2-1|. Du räknar ju t ex fram att derivatan har ett nollställe.
Marcus N skrev:Hondel skrev:Jag blev också förvirrad, på pappret har du högst upp skrivit abs(x-1), men i övrigt har du skrivit och räknat med abs (x^2-1)
Nej, uppgiften är f(x)=abs(x-1) inte abs(x^2-1).
Jag har ingen aning varför den andra volontärer vill beräkna (-1)^2 hela tiden.
Jag ska berätta varför hen vill det: du har skrivit att f(x)=abs(x^2-1) överallt, förutom på översta raden på pappret. Du har också räknat som att f(x)=abs(x^2-1) överallt.
Marcus N skrev:Ja, för att derivatan för ej def. på någon ändpunkten då ska dem inte vara med.
Nej exakt, men när du skrivit ned derivatan har du först skrivit det som att den är definierad i ändpunkterna, men sedan säger du att den inte är det. Jag menade bara att du ska skriva () istället för [] när du skriver derivatan, så att det blir samma överallt (att derivatan inte är definierad i ändpunkterna). Men det var en kommentar på hur du kan förbättra lösningen. Ditt största problem verkar vara att du räknat med fel funktion f







