Bestäm alfa

AB och AC är tangenter till cirkeln. Vilken storlek har då vinkeln ACM (M är mittpunkten)? Hur är det med ABM?

Smutstvätt skrev:

AB och AC är tangenter till cirkeln. Vilken storlek har då vinkeln ACM (M är mittpunkten)? Hur är det med ABM?

90 grader men hur vet jag det utan att det ser ut så?

En tangent parallell med objektet i punkten. Om du drar en punkt från tangeringspunkten till mittpunkten av en cirkel, kommer den linjen alltid att vara vinkelrät mot tangenten. :)

Smutstvätt skrev:

En tangent parallell med objektet i punkten. Om du drar en punkt från tangeringspunkten till mittpunkten av en cirkel, kommer den linjen alltid att vara vinkelrät mot tangenten. :)

hur vet man det?

Det finns säkert ett formellt bevis för detta, men det lättaste är nog att fundera på vad en tangent och en vinkelrät linje egentligen innebär. En förkunskap som krävs är vetskapen om att den kortaste sträckan från en punkt på en linje L, till en annan punkt P (i xy-planet) är att gå i en nittiogradig vinkel från någon punkt på linjen. Det låter krångligare än det är. Detta är en illustration av samma problem: 

Den kortaste vägen från linjen L till punkten J är den väg som är vinkelrät mot linjen L (och går genom J). Varför? Jo, eftersom det minimerar den sträcka vi går. Återigen, formella bevis finns säkert, men det är nog lättast att bara rita upp och prova med några olika värden.

På en cirkel ligger alla punkter lika långt ifrån mittpunkten. Vår tangent kommer alltså att tangera cirkeln i precis en punkt, och kommer att ha samma lutning som cirkeln har i just den punkten. Vi har därmed denna konstruktion:

Där A är cirkelns mittpunkt och B tangeringspunkten. Den ljuslila linjen tangerar cirkeln i B. 

Vi kan nu prova att gå från cirkelns mitt A, till olika punkter på tangentlinjen.

Om vi tittar på avståndet från A till tangentlinjen, ser vi att avståndet minskar när vi närmar oss tangeringspunkten B. I detta fall vill vi gå från A ut till cirkelns rand, men vi vill endast gå längden av cirkelns radie, i någon riktning, annars går vi ju utanför cirkeln. Den enda punkt som håller oss på cirkelns rand är den absolut kortaste sträckan till tangentlinjen. Inga andra av tangentens punkter ligger ju på cirkelns rand, och vi måste då gå längre än en radies längd. Den absolut kortaste sträckan från en punkt till en linje skar ju dock alltid linjen i en rät vinkel. Därmed måste linjen från en tangeringspunkt till mittpunkten vara vinkelrät mot tangentlinjen. 

Smutstvätt skrev:

Det finns säkert ett formellt bevis för detta, men det lättaste är nog att fundera på vad en tangent och en vinkelrät linje egentligen innebär. En förkunskap som krävs är vetskapen om att den kortaste sträckan från en punkt på en linje L, till en annan punkt P (i xy-planet) är att gå i en nittiogradig vinkel från någon punkt på linjen. Det låter krångligare än det är. Detta är en illustration av samma problem: 

Den kortaste vägen från linjen L till punkten J är den väg som är vinkelrät mot linjen L (och går genom J). Varför? Jo, eftersom det minimerar den sträcka vi går. Återigen, formella bevis finns säkert, men det är nog lättast att bara rita upp och prova med några olika värden.

På en cirkel ligger alla punkter lika långt ifrån mittpunkten. Vår tangent kommer alltså att tangera cirkeln i precis en punkt, och kommer att ha samma lutning som cirkeln har i just den punkten. Vi har därmed denna konstruktion:

Där A är cirkelns mittpunkt och B tangeringspunkten. Den ljuslila linjen tangerar cirkeln i B. 

Vi kan nu prova att gå från cirkelns mitt A, till olika punkter på tangentlinjen.

Om vi tittar på avståndet från A till tangentlinjen, ser vi att avståndet minskar när vi närmar oss tangeringspunkten B. I detta fall vill vi gå från A ut till cirkelns rand, men vi vill endast gå längden av cirkelns radie, i någon riktning, annars går vi ju utanför cirkeln. Den enda punkt som håller oss på cirkelns rand är den absolut kortaste sträckan till tangentlinjen. Inga andra av tangentens punkter ligger ju på cirkelns rand, och vi måste då gå längre än en radies längd. Den absolut kortaste sträckan från en punkt till en linje skar ju dock alltid linjen i en rät vinkel. Därmed måste linjen från en tangeringspunkt till mittpunkten vara vinkelrät mot tangentlinjen. 

oki tack så mkt!! hur kan jag tänka på b)?

Dra två radier, en från B och en från C, båda till mittpunkten. Det ger oss denna bild:

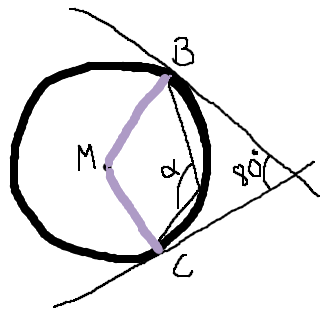
Nu har vi två fyrhörningar (egentligen tre, men men):

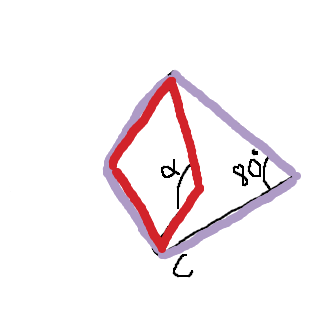
Börja med den lila fyrhörningen, hur stora är dess vinklar?

oki tack så mkt!! hur kan jag tänka på b)?

Gör en ny tråd för den frågan. Det står i Pluggakutens regler att varje tråd skall handla om en fråga, och du behöver inga värden från a-uppgiften för att kunna lösa uppgift b. /moderator