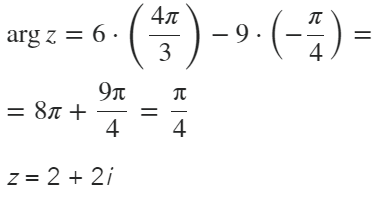Bestäm absolutbeloppet och argumentet

Hejsan, jag vet inte ens hur jag ska börja på denna problem...
Borde jag förenkla talet först?
Boken gör på detta sättet:
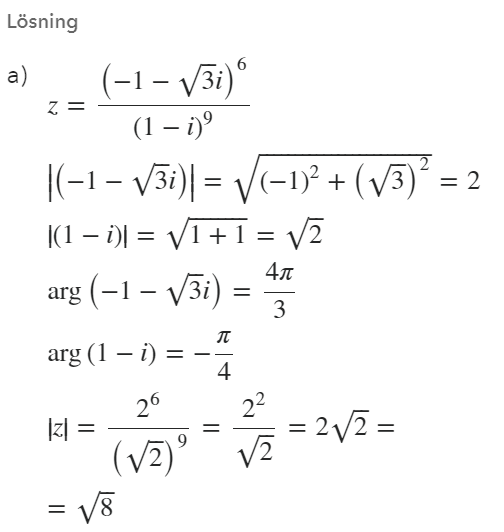
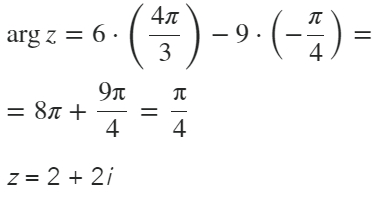
Men ärligt talat förstår jag inte alls vad som händer här.
Jag förstår typ vad de gör, men jag har aldrig ens sett en komplex tal som denna förr. De har inte förklarat hur man ska lösa en sån här uppgift!
Kunde någon ge mig lite tips?
Tompalomp skrev:
Hejsan, jag vet inte ens hur jag ska börja på denna problem...
Borde jag förenkla talet först?
Boken gör på detta sättet:
Men ärligt talat förstår jag inte alls vad som händer här.
Jag förstår typ vad de gör, men jag har aldrig ens sett en komplex tal som denna förr. De har inte förklarat hur man ska lösa en sån här uppgift!
Kunde någon ge mig lite tips?
De gör på det enklaste sättet, gör om till polär form och räknar med detta. För komplexa tal är det enklast att räkna addition och subtraktion med rektangulär form z = a+bi, och multiplikation och division med polär form.
Okej, då fattar jag. Om jag gör om de till polär form först:
talet z1 är i tredje kvadrant så argumentet måste vara
i polär form:
z2 är i fjärde kvadrant och är därför
här, kunde jag också ta?
Finns det någon skillnad? Båda är ju 315 grader, eller i andra fallet -45 grader. De borde ju vara samma?
Anyways, om jag tar
då får jag totalt:
vad är nästa steget?
Då kan du räkna ut belopp och argument för täljare respektive nämnare.
är jag på rätt håll eller gör jag helt fel nu?
Rätt håll!
Då återstår belopp och argument av kvoten.
hmm, vet inte exakt om jag fattar vad du säger. ska jag göra så här?
?
Ja, precis.
Jaha! Okej nice
men detta känns ju verkligen som jag har gjort något konstigt, eller?
Ta bort alla hela varv.
Förenkla även 4/sqrt(2).
Skulle detta vara lättare om jag bara använde istället för ?
Jag kan förenkla:
Men jag kommer fortfarande inte kunna få ut något fint nummer ur
Hade det varit lättare om jag använde istället?
Tompalomp skrev:Skulle detta vara lättare om jag bara använde istället för ?
...
Undersök! Vad får du för argument om du använder detta?
eller okej, om jag tar bort alla hela varv:
där tror jag jag fattade. glömde ta bort alla varven!