bestäm a utifrån triangelns area

Börja med att rita grafen till y = |ax+2|-2 för något värde på a (som är större än 0).

Markera triangeln i din figur och fundera på hur du ska kunna sätta upp ett uttryck för triangelns area.

Sätt detta uttryck lika med 3 och lös ut a.

Yngve skrev:

Börja med att rita grafen till y = |ax+2|-2 för något värde på a (som är större än 0).

Markera triangeln i din figur och fundera på hur du ska kunna sätta upp ett uttryck för triangelns area.

Sätt detta uttryck lika med 3 och lös ut a.

Inte så säker på hur jag ska gå tillväga för att rita grafen, men ser ju direkt att dens spets är förskjuten 2 steg till vänster och "-2" vet jag inte hur jag ska få med.

Arean för en triangel är bh/2 = 3, höjden bör vi få genom att kolla från skärningen till spetsen.

naturnatur1 skrev:

Inte så säker på hur jag ska gå tillväga för att rita grafen, men ser ju direkt att dens spets är förskjuten 2 steg till vänster och "-2" vet jag inte hur jag ska få med.

Sätt a = 1. Då blir y = |x+2|-2. Rita den grafen.

Arean för en triangel är bh/2 = 3, höjden bör vi få genom att kolla från skärningen till spetsen.

Det stämmer. Och basens längd får vi genom att beräkna avståndet mellan nollställena.

Yngve skrev:

naturnatur1 skrev:

Inte så säker på hur jag ska gå tillväga för att rita grafen, men ser ju direkt att dens spets är förskjuten 2 steg till vänster och "-2" vet jag inte hur jag ska få med.

Sätt a = 1. Då blir y = |x+2|-2. Rita den grafen.

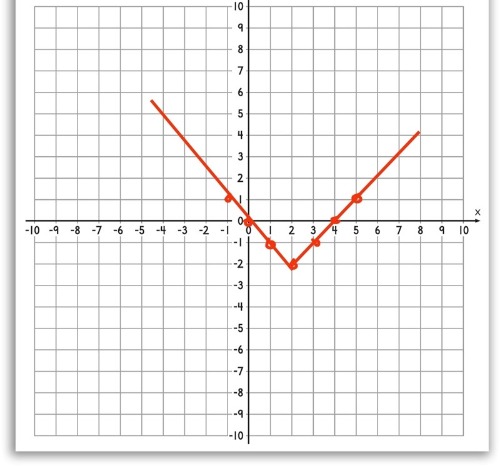
Den jag ritar för hand är inte samma som den i miniräknaren. Hur ska jag tänka när jag ska rita för hand?

Jag sätter in olika x-värden och sedan får jag fram y-värdet, 

säg att jag har x=1, då blir det

y = I 1-2 I -2 (alltså 1-2= -1) så (1, -1)

x= 2

y = l 2-2 l -2 = -2 (2,-2)

Dina uträkningar stämmer.

Hur blir det för x = 0, x = 3 och x = 4?

Visa gärna din handritade graf.

Yngve skrev:

Dina uträkningar stämmer.

Hur blir det för x = 0, x = 3 och x = 4?

Visa gärna din handritade graf.

Tillägg: 11 nov 2023 21:16

På miniräknaren ligger triangeln istället i tredje kvadranten, och inte fjärde.

Ooops, ser nu att du har räknat y = |x-2|+2 istället för y = |y+2|-2.

Och jag missade det.

Välj istället punkterna x = -4, x = -3, x = -2, x = -1 och x = 0.

Yngve skrev:

Ooops, ser nu att du har räknat y = |x-2|+2 istället för y = |y+2|-2.

Menar du x istället för y på sista?

Och jag missade det.

Välj istället punkterna x = -4, x = -3, x = -2, x = -1 och x = 0.

Hur vet man vilka punkter man ska ha? 

naturnatur1 skrev:

Menar du x istället för y på sista?

Ja, jag skrev fel.

Hur vet man vilka punkter man ska ha? 

Du kan välja fritt, men det lämpligt att ta punkten vid och ett par punkter på var sin sida av "brytpunkten", dvs den punkt där uttrycket innanför absolutbeloppstecknen är lika med 0. I det här fallet x = -2, eftersom -2+2 = 0.

Yngve skrev:

naturnatur1 skrev:

Menar du x istället för y på sista?

Ja, jag skrev fel.

Hur vet man vilka punkter man ska ha? 

Du kan välja fritt, men det lämpligt att ta punkten vid och ett par punkter på var sin sida av "brytpunkten", dvs den punkt där uttrycket innanför absolutbeloppstecknen är lika med 0. I det här fallet x = -2, eftersom -2+2 = 0.

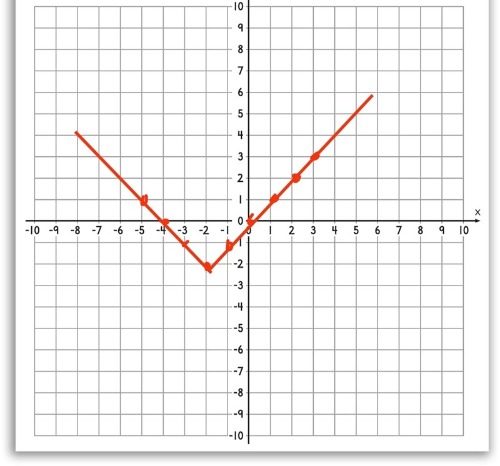
OK nu ser det bra ut.

Nu vill du hitta nollställena för att kunna beräkna längden av triangelns bas.

Då kan det vara praktiskt att först ta fram ekvationerna för de två räta linjerna.

Tips: Grafen harvett utseende då x > -2 och ett annat då x < -2.

Yngve skrev:

OK nu ser det bra ut.

Nu vill du hitta nollställena för att kunna beräkna längden av triangelns bas.

Då kan det vara praktiskt att först ta fram ekvationerna för de två räta linjerna.

Tips: Grafen harvett utseende då x > -2 och ett annat då x < -2.

Jag håller helt med om din metod.

Men går inte det direkt att se att 0 och -4 är nollställena? m.a.o en bas på 4 l.e

Jo, men din graf är ju ritad baserat på att a = 1.

Om a är något annat tal så har linjerna en annan lutning och de skär då x-axeln på andra ställen.

Du behöver nu

1. Ta fram linjernas ekvationer. Dessa beror på a.
2. Bestämma avståndet mellan nollställena. Detta beror på a.
3. Sätta upp ett uttryck för triangelns area. Denna beror på a.
4. Sätta detta uttryck lika med 3 och lösa ut a.

Då x är större än -2:

y = x 

Då x är mindre än -2:

y = -x - 4

Nu svarade jag kanske på ekvationerna för de som finns i grafen? Hur ska jag tänka för a?

y = l ax +2 l -2 

naturnatur1 skrev:

Då x är större än -2:

y = x 

Då x är mindre än -2:

y = -x - 4

Nu svarade jag kanske på ekvationerna för de som finns i grafen?

Ja, det gjorde du, alltså för a = 1.

Hur ska jag tänka för a?

y = l ax +2 l -2 

Är du med på att följande gäller för absolutbelopp?

• $|b|=b$ om $b\geq0$
• $|b|=-b$ om $b<0$

Det betyder att

• $|ax+2|=ax+2$ då $ax+2\geq0$, dvs då $ax\geq-2$, dvs då $x\geq-\frac{2}{a}$ (eftersom $a>0$).
• $|ax+2|=-(ax+2)$ då $ax+2<0$, dvs då $ax<-2$, dvs då $x<-\frac{2}{a}$ (eftersom $a>0$).

Nu är du nära att bestämma ekvationerna för de två linjerna.

Yngve skrev:

Hur ska jag tänka för a?

y = l ax +2 l -2 

Är du med på att följande gäller för absolutbelopp?

• $|b|=b$ om $b\geq0$
• $|b|=-b$ om $b<0$

Ja det är jag.

Det betyder att

• $|ax+2|=ax+2$ då $ax+2\geq0$, dvs då $ax\geq-2$, dvs då $x\geq-\frac{2}{a}$ (eftersom $a>0$).
• $|ax+2|=-(ax+2)$ då $ax+2<0$, dvs då $ax<-2$, dvs då $x<-\frac{2}{a}$ (eftersom $a>0$).

Nu är du nära att bestämma ekvationerna för de två linjerna.

Jag tror jag hänger med. Men jag förstår bara inte hur jag ska ställa upp det? Och varför vi ställer upp dessa "samband",  (för att få reda på a ja) men inte hur det leder oss till a?

För båda linjerna gäller att y = |ax+2|-2.

• Till vänster om "brytpunkten" x = -2/a gäller att |ax+2| = -(ax+2) = -ax-2, vilket innebär att ekvationen för den räta linjen är y = -ax-2-2, dvs y = -ax-4. Ta nu reda på var denna linje skär x-axeln, dvs var nollstället till y = -ax-4 ligger.
• Till höger om "brytpunkten" x = -2/a gäller att |ax+2| = ax+2, vilket innebär att ekvationen för den räta linjen är y = ax+2-2, dvs y = ax. Ta nu reda på var denna linje skär x-axeln, dvs var nollstället till y = ax ligger.

Avståndet mellan dessa två nollställen är lika med längden av triangelns bas.

Tack Yngve för din hjälp. Det löste sig nu!