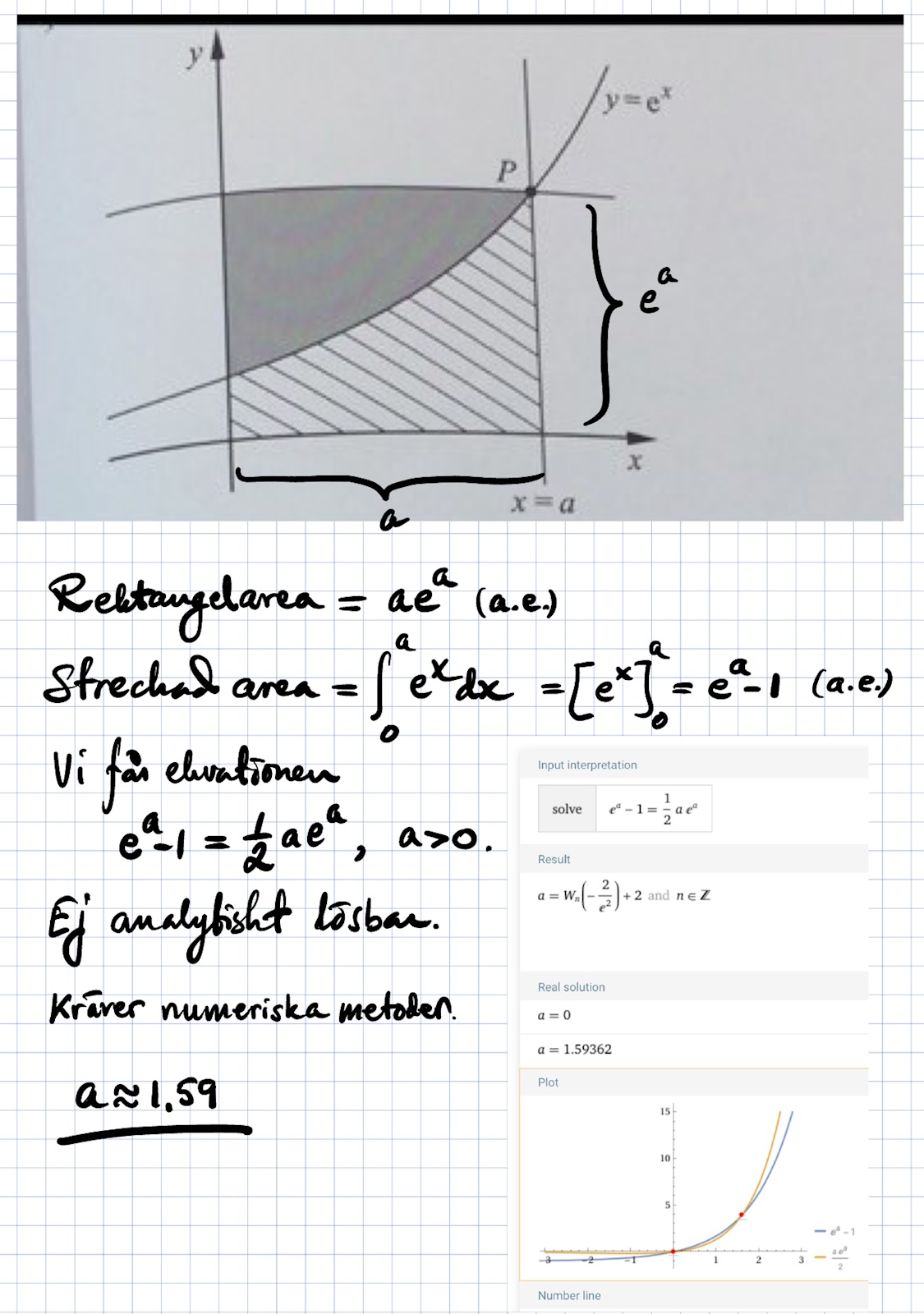
bestäm a så att arean.. (Matematik/Matte 5)

Har du kommit fram till något uttryck för de två olika areorna?

Stokastisk skrev :
Har du kommit fram till något uttryck för de två olika areorna?

nej är helt borta..

Känner du till att du kan få arean under kurvan y = e^x genom att integrera?

Stokastisk skrev :
Känner du till att du kan få arean under kurvan y = e^x genom att integrera?

men snälla kan du lägga upp en bild och visa för kan inte föreställa mig hur det ska se ut

Jag vet inte vad jag skulle visa i den bilden? Du får arean av området under grafen y = e^x och mellan x = 0 till x = a genom att beräkna integralen

$\int_{0}^{a} e^{x} d x$

Sedan får du arean av det övre området, dvs det mellan y = a och y = e^x samt x = 0 till x = a genom att beräkna integralen

$\int_{0}^{a} (a - e^{x}) d x$

Så börja med att beräkna dessa integraler.

Stokastisk skrev :
Jag vet inte vad jag skulle visa i den bilden? Du får arean av området under grafen y = e^x och mellan x = 0 till x = a genom att beräkna integralen
$\int_{0}^{a} e^{x} d x$
Sedan får du arean av det övre området, dvs det mellan y = a och y = e^x samt x = 0 till x = a genom att beräkna integralen
$\int_{0}^{a} (a - e^{x}) d x$
Så börja med att beräkna dessa integraler.

har försökt integrera den första och fick den till (e^x*a^2)/ 2

är det på något sätt rätt?

Nej det stämmer inte. Utan försök bestäm en primitiv funktion F till e^x, sedan använder du att

$\int_{0}^{a} e^{x} d x = F (a) - F (0)$ .

Så första steget i att integrera detta är att bestämma en primitiv funktion F.

Stokastisk skrev :
Nej det stämmer inte. Utan försök bestäm en primitiv funktion F till e^x, sedan använder du att
$\int_{0}^{a} e^{x} d x = F (a) - F (0)$ .
Så första steget i att integrera detta är att bestämma en primitiv funktion F.

kan du visa på den första så gör jag den andra, för då är det enklare att följa stegen

En primitiv funktion till e^x är en funktion vars derivata är e^x. Känner du till någon funktion vars derivata är e^x?

Stokastisk skrev :
En primitiv funktion till e^x är en funktion vars derivata är e^x. Känner du till någon funktion vars derivata är e^x?

nej,,

Derivatan för e^x är e^x, så alltså är e^x en primitiv funktion till e^x. Därför får man att

$\int_{0}^{a} e^{x} d x = e^{a} - e^{0} = e^{a} - 1 .$

Stokastisk skrev :
Derivatan för e^x är e^x, så alltså är e^x en primitiv funktion till e^x. Därför får man att
$\int_{0}^{a} e^{x} d x = e^{a} - e^{0} = e^{a} - 1 .$

f(x) = e^x

f'(x)= e^x

och sen?

elevensombehöverhjälp skrev :
Stokastisk skrev :
Derivatan för e^x är e^x, så alltså är e^x en primitiv funktion till e^x. Därför får man att
$\int_{0}^{a} e^{x} d x = e^{a} - e^{0} = e^{a} - 1 .$
f(x) = e^x
f'(x)= e^x
och sen?

Fast du behöver ju inte derivera f(x), utan du ska hitta en primitiv funktion F. En primitiv funktion till f(x) är F(x) = e^x. Detta eftersom man då får att

F'(x) = e^x = f(x)

Så alltså är F(x) en primitiv funktion till f(x). Du ska nu beräkna integralen med hjälp av denna primitiva funktion (jag gjorde visserligen det i inlägget du citerade).

Stokastisk skrev :
elevensombehöverhjälp skrev :
Stokastisk skrev :
Derivatan för e^x är e^x, så alltså är e^x en primitiv funktion till e^x. Därför får man att
$\int_{0}^{a} e^{x} d x = e^{a} - e^{0} = e^{a} - 1 .$
ja men då har man ju beräknat integralen med hjälp av den primitiva funktionen,, är man klar nu?

elevensombehöverhjälp skrev :
Stokastisk skrev :
elevensombehöverhjälp skrev :
Stokastisk skrev :
Derivatan för e^x är e^x, så alltså är e^x en primitiv funktion till e^x. Därför får man att
$\int_{0}^{a} e^{x} d x = e^{a} - e^{0} = e^{a} - 1 .$
ja men då har man ju beräknat integralen med hjälp av den primitiva funktionen,, är man klar nu?

Nej du är inte klar, uppgiften är ju att beräkna för vilket a som areorna blir lika. Nu har du bara beräknat arean av det undre området. Du behöver även beräkna arean för det övre området, och sedan lösa för vilket a som dessa två areor är lika.

Sedan får du arean av det övre området, dvs det mellan y = a och y = e^x samt x = 0 till x = a genom att beräkna integralen
$\int_{0}^{a} (a - e^{x}) d x$
Så börja med att beräkna dessa integraler.

ska jag integrera uttrcktet ovan?

elevensombehöverhjälp skrev :
Sedan får du arean av det övre området, dvs det mellan y = a och y = e^x samt x = 0 till x = a genom att beräkna integralen
$\int_{0}^{a} (a - e^{x}) d x$
Så börja med att beräkna dessa integraler.

ska jag integrera uttrcktet ovan?

Ja, fast jag ser att jag gjorde en miss i det där uttrycket, det ska vara

$\int_{0}^{a} (e^{a} - e^{x}) d x$

om jag integrerar det får jag det till e^a *a- e^a + 1

rätt så?

Det är korrekt, nu måste du lösa när ae^a - e^a + 1 = e^a - 1, detta måste du göra numeriskt.

Stokastisk skrev :
Det är korrekt, nu måste du lösa när ae^a - e^a + 1 = e^a - 1, detta måste du göra numeriskt

numeriskt?

elevensombehöverhjälp skrev :
Stokastisk skrev :
Det är korrekt, nu måste du lösa när ae^a - e^a + 1 = e^a - 1, detta måste du göra numeriskt

numeriskt?

Ja, du kommer inte kunna räkna ut det algebraiskt. Så om ni inte gått igenom någon metod att lösa ekvationer numerisk (som Newton-Raphsons metod) så kan du säkert använda dig av en grafräknare för att få fram en lösning.

Jag vet inte hur man gör det på räknaren, jag har en sån:

Har inte en sådan där miniräknare, men om jag gissar.

1. Tryck på knappen "Y = ", på Y1 skriver du in X*e^(X) - e^(X) + 1 och på Y2 skriver du in e^(X) - 1.

2. Gå in på "Calc" (tryck på "2ND" och sedan "TRACE")

3. Välj intersect

4. Välj de två kurvorna du ska beräkna skärningen mellan.

5. Välj en gissning var du tror att lösningen är, denna gissning ska vara nära där kurvorna skär varandra.

Sedan löser miniräknaren ekvationen åt dig.

Stokastisk skrev :
Har inte en sådan där miniräknare, men om jag gissar.
1. Tryck på knappen "Y = ", på Y1 skriver du in X*e^(X) - e^(X) + 1 och på Y2 skriver du in e^(X) - 1.
2. Gå in på "Calc" (tryck på "2ND" och sedan "TRACE")
3. Välj intersect
4. Välj de två kurvorna du ska beräkna skärningen mellan.
5. Välj en gissning var du tror att lösningen är, denna gissning ska vara nära där kurvorna skär varandra.
Sedan löser miniräknaren ekvationen åt dig.

så långt har jag lyckats

Det ser inte ut som du har skrivit in Y2 korrekt, om du fixar till det och fortsätter till det där steget, så är det bara att trycka enter. Sedan kommer den fråga dig om Y2 är den andra kurvan, tryck enter. Sedan kommer den fråga "Guess?" där så trycker du på piltangenterna så att du får krysset ungefär där kurvorna skär varandra, sedan trycker du enter.

Stokastisk skrev :
Det ser inte ut som du har skrivit in Y2 korrekt, om du fixar till det och fortsätter till det där steget, så är det bara att trycka enter. Sedan kommer den fråga dig om Y2 är den andra kurvan, tryck enter. Sedan kommer den fråga "Guess?" där så trycker du på piltangenterna så att du får krysset ungefär där kurvorna skär varandra, sedan trycker du enter.

kan du fota av hur du får det på din?

Jag har inget att fota av den med på ett enkelt sätt. Men jag såg nu att du nog också skrivit in fel funktion för Y1. Se till så du skriver in rätt funktioner för både Y1 och Y2.

Stokastisk skrev :
Jag har inget att fota av den med på ett enkelt sätt. Men jag såg nu att du nog också skrivit in fel funktion för Y1. Se till så du skriver in rätt funktioner för både Y1 och Y2.

men vad blir svaret?

Jag får svaret till 1.59. Om du gjort allt rätt på miniräknaren bör du få fram det längst ned till vänster i displayen.

Stokastisk skrev :
Jag får svaret till 1.59. Om du gjort allt rätt på miniräknaren bör du få fram det längst ned till vänster i displayen.

fick det nu!!, hade som du sa skrivit in fel värde i både y1 och y2, tack,, nu har jag lärt mig detta.

och i så fall är 1,59 är då a de letar efter i uppg visst?

Ja, det är korrekt, men det ska vara tre decimalers noggrannhet, så en decimal till får du ta med.

Stokastisk skrev :
Ja, det är korrekt, men det ska vara tre decimalers noggrannhet, så en decimal till får du ta med.

jag fick det till 1,594 och du?

Japp jag får samma sak.