Bestäm a och b så att f(x) blir deriverbar i punkten

Uppgiften ser ut så här:

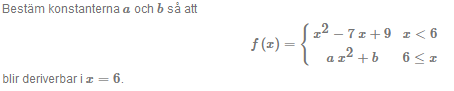
När jag försöker lösa den så tar jag först vänstergränsvärdet när x går mot 6 på det övre uttrycket, och får det till 3. Jag vill alltså att den nedre funktionen ska vara lika med 3 i x=6. Då sätter jag in x=6 i den och sätter hela lika med 3. Sedan kan man bestämma konstanterna a och b hur man vill tänker jag, så jag sätter a=1 och får b=-33, men svaret stämmer tydligen inte.

Hur har jag tänkt fel?