Bestäm a och b
Hej
Jag ska lösa den här
![]()
Och har gjort såhär

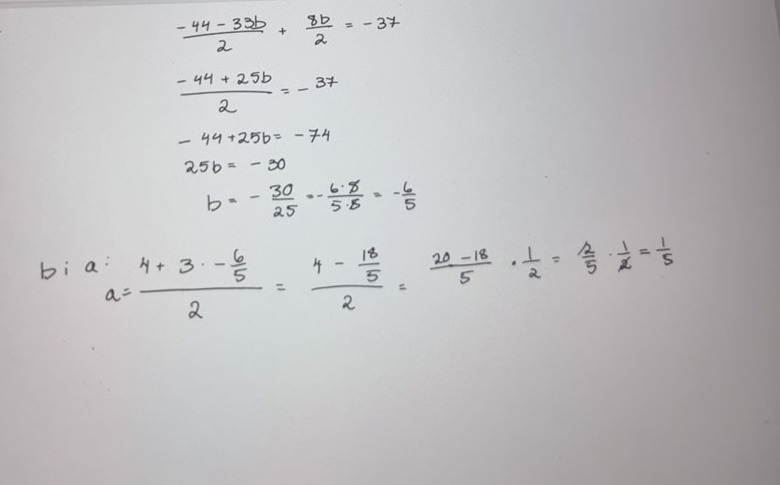
Men a ska vara 4 och b ska vara 2. Vad har jag gjort för fel? (Ska jag ens göra såhär här)
Hej.
Du kan göra som du har gjort, men det blir, som du upptäcker, en ganska lång och därmed felbenägen lösning.
Jag rekommenderar dig att istället använda det faktum att eftersom polynomekvationen har reella koefficienter så förekommer eventuella komplexa rötter i komplexkonjugerade par.
Det innebär att eftersom är en rot så är även en rot.
Detta innebär i sin tur att både och är faktorer i polynomet .
Du kan då använda polynomdivision för att faktorisera polynomet.
Ännu bättre är nog att du använder sambandet mellan rötter och koefficienter som du hittar I din bok.
Yngve skrev:Hej.
Du kan göra som du har gjort, men det blir, som du upptäcker, en ganska lång och därmed felbenägen lösning.
Jag rekommenderar dig att istället använda det faktum att eftersom polynomekvationen har reella koefficienter så förekommer eventuella komplexa rötter i komplexkonjugerade par.
Det innebär att eftersom är en rot så är även en rot.
Detta innebär i sin tur att både och är faktorer i polynomet .
Du kan då använda polynomdivision för att faktorisera polynomet.
Ännu bättre är nog att du använder sambandet mellan rötter och koefficienter som du hittar I din bok.
Tack ska läsa på lite🥹


