beräkning av en cylinders volymökning med integraler
En vacker vårkväll tänker surströmmingsälskaren Anders avnjuta innehållet i en burk som han köpt förra sommaren. Under vintern har burkens botten och lock börjat bukta ut eftersom innehållet jäser. Det som från början kunde beskrivas som en rak cirkulär cylinder, med diametern 12,0 cm och höjden 5,0 cm är nu en kropp som från sidan ser ut som på bilden nedan.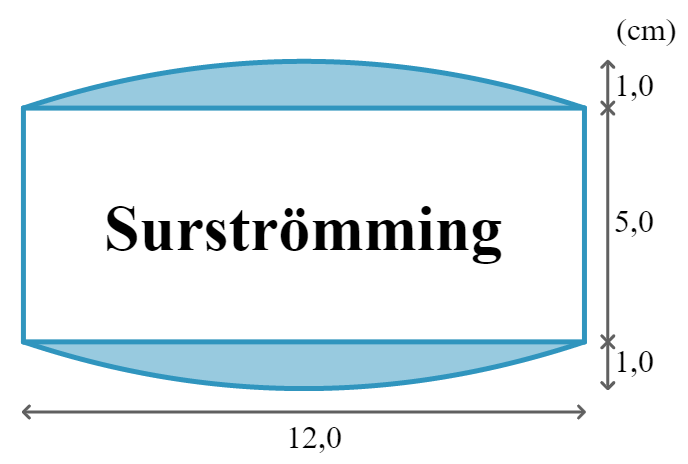
Anders observerar att lockets, och även bottnens, ”profil” ganska exakt kan beskrivas med grafen till en andragradsfunktion av typen y=ax2+bx+c. Beräkna volymökningen i procent, när burken svällt så att den buktar ut 1,0 cm på varje sida samtidigt som diameter och kanthöjd är oförändrade.
Jag hittade den här funktionen: y= -x2/36 + x/3 men jag förstår inte varför dem räknar volymen runt y-axeln och inte x-axeln.
Du kan göra på båda sätt, men om du använder x^2 kurva är rot. runt y-axel enklare.
Din kurvar verkar konstigt, utan närmare förklaring. Lägg botten på x-axeln och mitt över y-axlen så skall
y=kx^2-1
för något k, sådant att y(6)=0.
Locket är en kopia, så den kan du glömma och mitten är en trivial cylinder som det finns formel för.
Det här fixar du. Rita och tänk lite.
