7
svar
97
visningar
Beräknar gränsvärdet då x->pi av funktionerna
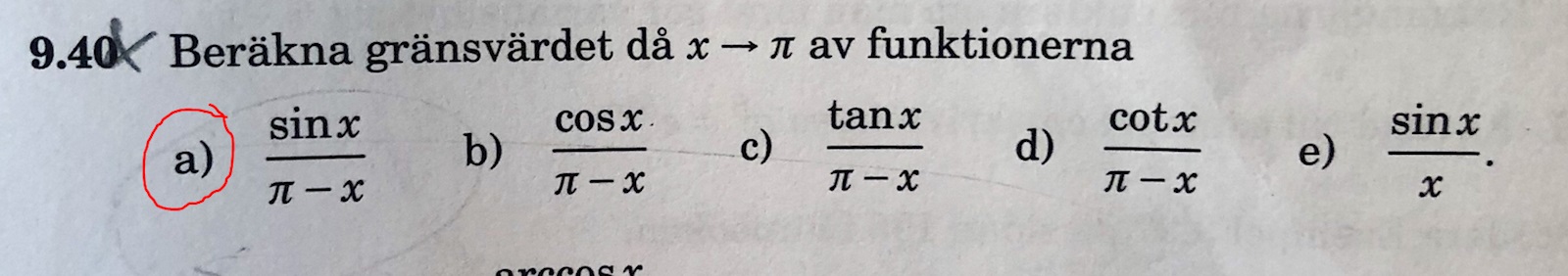
Hur kan vi skriva om uttrycket så nämnaren inte bli 0 när vi beräknar gränsvärdet.
Så här gjort ja:

Det såg jätte bra ut tills du applicerade L'hopitals. Den behövs inte och om du ändå tänkt använda den regeln, varför gjorde du inte det från början?
du har ju redan 0/0 när du stoppar in pi.
Nog vet du vad kan förenklas till? annars är det bara ta fram enhetscirkeln.
Menar du att ja kan använda den här formeln:
Men jag kommer ändå får t=0 på nämnare.
För att nämnare är bara t och den ska går emot noll.
Precis, du har att
Nu har du ju ett standardgränsvärde, eller hur? Kika i formelbladet. :)
Nästan, men ska väl inte gå mot ?



