Beräknar gränsvärdena x-> oändligheten
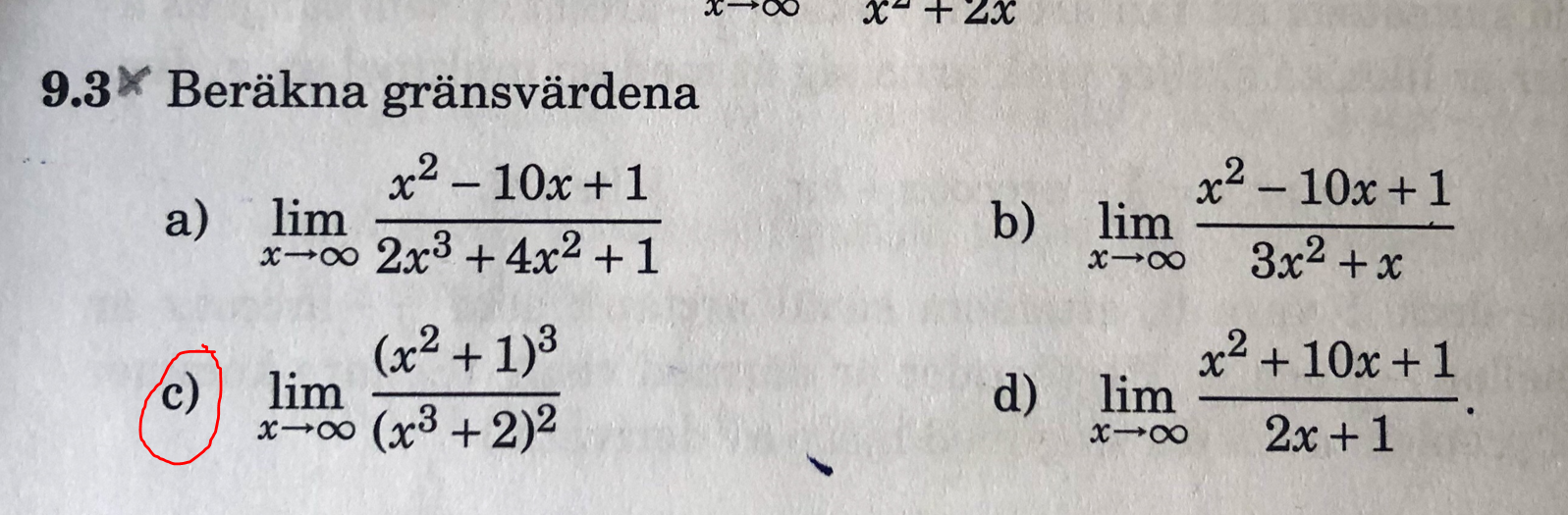
Hur lösa man c)?
Facit:
Expandera och identifiera den dominerande faktorn.
Eller så gissar vi baserat på polynomen och potenserna
Vilken är den dominerad faktor??
För ett godtyckligt stort x kan vi säga att:
och att
Du får alltså .
Dracaena skrev:För ett godtyckligt stort x kan vi säga att:
och att
Du får alltså .
?
Grejen är att koefficienterna för polynomen är 1 så vi kommer endast producera en i täljaren och nämnaren. om betecknar graden av ett polynom så är resten så att , så när de divideras med går allting mot 0. Det enda som spelar roll är alltså hur många vi har, och vi har en st i täljaren och nämnaren vilket leder till .
Har jag tänkt rätt i #6?
Ja, det ser bra ut. Fårgan är väl bara hur rigoröst man vill att du ska visa att det faktiskt går mot 1. I värsta fall kan man bara expandera med Pascals triangel och sedan dividera med den dominerande faktorn.
= = = =
Snyggt PATENTERAMERA! Det var en fiffig omskrivning. :)




