32 svar

1141 visningar

Vanessa_malmkvist behöver inte mer hjälp

beräkna z1 och z2

frågan lyder som följande:

$z_{1} = \cos \frac{π}{6} + i \sin \frac{π}{6} z_{2} = \cos \frac{7 π}{6} + i \sin \frac{7 π}{6}$

a) beräkna z1z2, och svara på rektangulär form - här skall man väll: $(\cos \frac{π}{6} + i \sin \frac{π}{6}) * (\cos \frac{7 π}{6} + i \sin \frac{7 π}{6})$

b)beräkna z2/z1 , svara på rektangulär form - här skall man väll: $\frac{(\cos \frac{7 π}{6} + i \sin \frac{7 π}{6})}{(\cos \frac{π}{6} + i \sin \frac{7 π}{6})}$

Hej

Om du skulle ha haft t.ex.

$z_{1} = \cos (v_{1}) + i \sin (v_{1}) z_{2} = \cos (v_{2}) + i \sin (v_{2})$

Det ger att $z_{1} \cdot z_{2} = \cos (v_{1} + v_{2}) + i \sin (v_{1} + v_{2})$ och $\frac{z_{2}}{z_{1}} = \cos (v_{2} - v_{1}) + i \sin (v_{2} - v_{1})$

Kommer du vidare?

jonis10 skrev:
Hej
Om du skulle ha haft t.ex.
$z_{1} = \cos (v_{1}) + i \sin (v_{1}) z_{2} = \cos (v_{2}) + i \sin (v_{2})$
Det ger att $z_{1} \cdot z_{2} = \cos (v_{1} + v_{2}) + i \sin (v_{1} + v_{2})$ och $\frac{z_{2}}{z_{1}} = \cos (v_{2} - v_{1}) + i \sin (v_{2} - v_{1})$
Kommer du vidare?

$\cos (\frac{π}{6} + \frac{7 π}{6}) + i \sin (\frac{π}{6} + \frac{7 π}{6}) s å p å a ? o c h p å b) \cos (\frac{7 π}{6} - \frac{π}{6}) + i \sin (\frac{7 π}{6} - \frac{π}{6}) s å ?$

Ja men du kan förenkla det mer!

jonis10 skrev:
Ja men du kan förenkla det mer!

på a) fick jag $- \sqrt[3]{- 1}$ , kan det stämma?

och b) fick jag till -1, kan det stämma?

känns inte som att jag förenklat på rätt vis..

Börja med att förenkla i polära koordinater innan du går över till rektangulära.

$a) \cos (\frac{π}{6} + \frac{7 π}{6}) + i \sin (\frac{π}{6} + \frac{7 π}{6}) b) \cos (\frac{7 π}{6} - \frac{π}{6}) + i \sin (\frac{7 π}{6} - \frac{π}{6})$

hur gör jag det till polär?

Du har redan polära koordinater. Förenkla parenteserna.

Smaragdalena skrev:
Du har redan polära koordinater. Förenkla parenteserna.

a) $\cos (\frac{4 π}{3}) + i \sin (\frac{4 π}{3})$

b) $\cos (π) + isin (π)$

så?

Markera ut talen i komplexa talplanet och kolla vad de har för rektangulära koordinater.

Smaragdalena skrev:
Markera ut talen i komplexa talplanet och kolla vad de har för rektangulära koordinater.

hur är det möjligt att markera in 4pi/3 i ett komplext talplan?

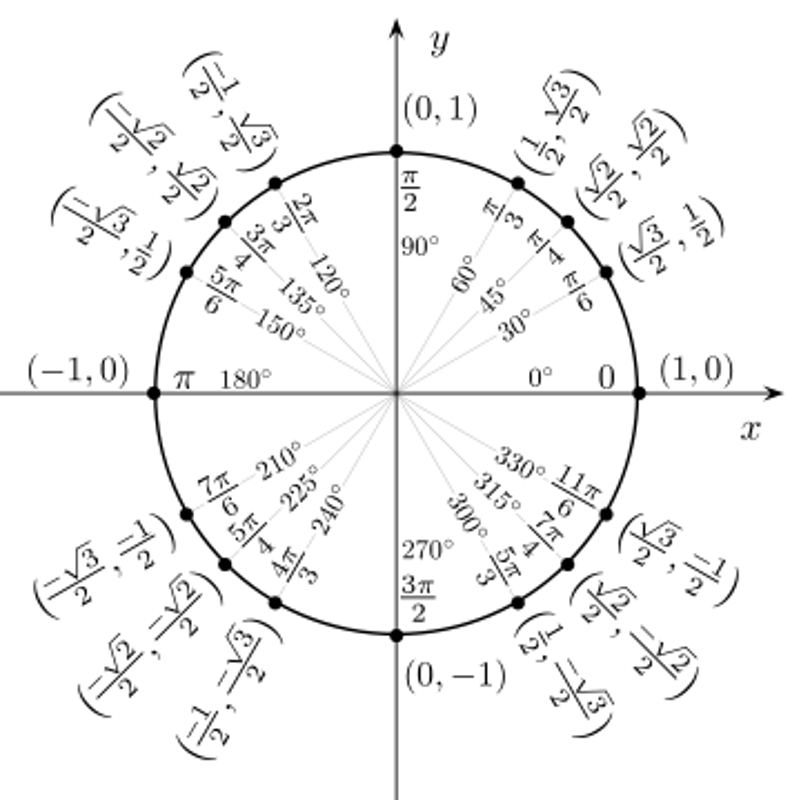
Båda dina tal har absolutbeloppet 1. Läs om komplexa tal i polär form här.

Euler:

$e^{i ϕ} = \cos (ϕ) + i \sin (ϕ)$

Smaragdalena skrev:
Båda dina tal har absolutbeloppet 1. Läs om komplexa tal i polär form här.

och argumentet är $\frac{4 π}{3}$

sen då?

b) $\cos (π) + isin (π)$

a) $\cos (\frac{4 π}{3}) + i \sin (\frac{4 π}{3})$

a) $\cos (- \frac{1}{2}) + i \sin (- \frac{\sqrt{3}}{2})$ , så?

Vanessa_malmkvist skrev:
Smaragdalena skrev:
Båda dina tal har absolutbeloppet 1. Läs om komplexa tal i polär form här.
och argumentet är $\frac{4 π}{3}$
sen då?

Börja med att läsa det avsnitt som Smaragdalena länkade till. Fråga sedan här om de delar du inte förstod.

a) $\cos (\frac{4 π}{3}) + i \sin (\frac{4 π}{3})$
b) $\cos (π) + isin (π)$

men jag har ju redan skrivit det i polär form?

Affe Jkpg skrev:
Euler:
$e^{i ϕ} = \cos (ϕ) + i \sin (ϕ)$

$e^{i ϕ_{1}} = \cos (ϕ_{1}) + i \sin (ϕ_{1}) e^{i ϕ_{2}} = \cos (ϕ_{2}) + i \sin (ϕ_{2}) \frac{e^{i ϕ_{1}}}{e^{i ϕ_{2}}} = e^{i (ϕ_{1} - ϕ_{2})} e^{i ϕ_{1}} e^{i ϕ_{2}} = e^{i (ϕ_{1} + ϕ_{2})}$

Affe Jkpg skrev:
Affe Jkpg skrev:
Euler:
$e^{i ϕ} = \cos (ϕ) + i \sin (ϕ)$
$e^{i ϕ_{1}} = \cos (ϕ_{1}) + i \sin (ϕ_{1}) e^{i ϕ_{2}} = \cos (ϕ_{2}) + i \sin (ϕ_{2}) \frac{e^{i ϕ_{1}}}{e^{i ϕ_{2}}} = e^{i (ϕ_{1} - ϕ_{2})} e^{i ϕ_{1}} e^{i ϕ_{2}} = e^{i (ϕ_{1} + ϕ_{2})}$

Vanessa_malmkvist skrev:
a) $\cos (\frac{4 π}{3}) + i \sin (\frac{4 π}{3})$
b) $\cos (π) + isin (π)$

men jag har ju redan skrivit det i polär form?

Uppgiften är att svara i rektangulär form. Använd enhetscirkeln jag skickade tidigare för att hitta exakta värden.

a) $\cos (- \frac{1}{2}) + i \sin (- \frac{\sqrt{3}}{2})$ , så?

för i enheltcirkeln så står det för cos respektive sin eller är det 240grader jag skall utgå ifrån?

Vanessa_malmkvist skrev:
a) $\cos (- \frac{1}{2}) + i \sin (- \frac{\sqrt{3}}{2})$ , så?
för i enheltcirkeln så står det för cos respektive sin eller är det 240grader jag skall utgå ifrån?

Vad är $cos(4\pi /3)$ ? (det är inte $cos(-1/2)$ )

Vad är $s i n (4 π / 3)$ ? (det är inte $sin(-\sqrt{3}/2)$ )

Yngve skrev:
Vanessa_malmkvist skrev:
a) $\cos (- \frac{1}{2}) + i \sin (- \frac{\sqrt{3}}{2})$ , så?
för i enheltcirkeln så står det för cos respektive sin eller är det 240grader jag skall utgå ifrån?
Vad är $cos(4\pi /3)$ ? (det är inte $cos(-1/2)$ )
Vad är $s i n (4 π / 3)$ ? (det är inte $sin(-\sqrt{3}/2)$ )

a)cos( $- \frac{1}{\sqrt{2}}$ )+isin( $\frac{1}{\sqrt{2}}$ )

så nu håller vi tummarna att det skall vara rätt!

b) $\cos (π) + isin (π)$

$\cos (- 1) + i \sin (0)$

detta gäller för b

Du skall svara i rektangulär form, d v s på formen z = a+bi.

Vanessa_malmkvist skrev:
Affe Jkpg skrev:
Affe Jkpg skrev:
Euler:
$e^{i ϕ} = \cos (ϕ) + i \sin (ϕ)$
$e^{i ϕ_{1}} = \cos (ϕ_{1}) + i \sin (ϕ_{1}) e^{i ϕ_{2}} = \cos (ϕ_{2}) + i \sin (ϕ_{2}) \frac{e^{i ϕ_{1}}}{e^{i ϕ_{2}}} = e^{i (ϕ_{1} - ϕ_{2})} e^{i ϕ_{1}} e^{i ϕ_{2}} = e^{i (ϕ_{1} + ϕ_{2})}$
?

Exempel:

$\frac{10^{4}}{10^{3}} = 10^{4 - 3} = 10^{1} = 10$
$\frac{e^{i \frac{7 π}{6}}}{e^{i \frac{π}{6}}} = e^{i (\frac{7 π}{6} - \frac{π}{6})} = e^{i π} = \cos (π) + i \sin (π)$

Smaragdalena skrev:
Du skall svara i rektangulär form, d v s på formen z = a+bi.

jag förstår det, men du sa att jag skulle ta fram exakta värde först

Vanessa_malmkvist skrev:
Smaragdalena skrev:
Du skall svara i rektangulär form, d v s på formen z = a+bi.
jag förstår det, men du sa att jag skulle ta fram exakta värde först

Ja och det exakta värdet på cos(pi) är -1, inte cos(-1).

På samna sätt är det exakta värdet av sin(pi) lika med 0, inte sin(0) (även om det råkar vara samma sak i just detta fallet)

Yngve skrev:
Vanessa_malmkvist skrev:
Smaragdalena skrev:
Du skall svara i rektangulär form, d v s på formen z = a+bi.
jag förstår det, men du sa att jag skulle ta fram exakta värde först
Ja och det exakta värdet på cos(pi) är -1, inte cos(-1).
På samna sätt är det exakta värdet av sin(pi) lika med 0, inte sin(0) (även om det råkar vara samma sak i just detta fallet)

så skall jag helt och hållet ta bort cos respektive sin och skriva -1+i*0 på b?

och $- \frac{1}{\sqrt{2}} + i \frac{1}{\sqrt{2}}$

är detta rätt?

känns som att jag för en gång skull gjort rätt, kan någon kontrollera att $- \frac{1}{\sqrt{2}} + i \frac{1}{\sqrt{2}} ä r o r g i n a l u t t r y c k e t a) i i r e k \tan g u l ä r f o r m ? o c h - 1 + i * 0 ä r s v a r e t i r e k \tan g u l ä r f o r m p å b ?$

Vanessa_malmkvist skrev:
känns som att jag för en gång skull gjort rätt, kan någon kontrollera att $- \frac{1}{\sqrt{2}} + i \frac{1}{\sqrt{2}} ä r o r g i n a l u t t r y c k e t a) i i r e k \tan g u l ä r f o r m ? o c h - 1 + i * 0 ä r s v a r e t i r e k \tan g u l ä r f o r m p å b ?$

a) $z_1\cdot z_2=cos(\frac{3\pi }{4})+isin(\frac{3\pi }{4})$

Eftersom $cos(\frac{3\pi }{4})=-\frac{1}{2}$ och $sin(\frac{3\pi }{4})=-\frac{\sqrt{3}}{2}$ så är $z_1\cdot z_2=-\frac{1}{2}-\frac{\sqrt{3}}{2}i$

b)-uppgiften är rätt.

Svara

Visa senaste svar