Beräkna volymen av en tetraeder om vi känner igen koordinaterna av dess hörn? Linjär algebra

Hej! Jag hade försökt lösa denna uppgift på ett annat sätt än facit och får fel svar. Är något av mitt tänk i uträkningen rätt eller blir alla stegen fel?

Jag tänkte att punkterna är:

A = (1,0,0), B = (1,2,0), C =(2,2,2) & D =(0,3,2)

Jag tänker mig att botten/basen av tetraedern utgörs av triangeln som bildas av B-C-D samt att höjden utgörs av ||A||. 

Tetraederns volym V = Basen*arean/3

Höjden = ||A|| = $\sqrt{1^2+0^2+0^2}$= 1

Triangelns area = parallelogramets area till triangeln dividerat med 2. dvs. ||BD x BC||/2

BD = (-1,1,2)

BC = (1,0,2)

BD x BC = $\left[\begin{array}{c}-1\\ 1\\ 2\end{array}\right]$x$\left[\begin{array}{c}1\\ 0\\ 2\end{array}\right]$= $\left[\begin{array}{c}\left|\begin{array}{cc}1& 0\\ 2& 2\end{array}\right|\\ \left|-\begin{array}{cc}-1& 1\\ 2& 2\end{array}\right|\\ \left|\begin{array}{cc}-1& 1\\ 1& 0\end{array}\right|\end{array}\right]$=$\left[\begin{array}{c}2\\ 4\\ -1\end{array}\right]$

Triangelns area blir därmed:

||BD x BC||/2 = $\sqrt{2^2+4^2+{(-1)}^2}$/2=$\sqrt{4+16+1}$/2=$\sqrt{21}$/2 a.e

Jag får då fram att volymen på tetraedern blir:

V = Basen*arean/3 = ($\sqrt{21}$/2*1)/3 = $\sqrt{21}$/6 volymenheter

 

Facit

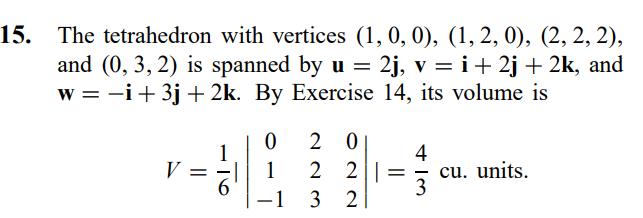
Facit refererar även till uppg.14

Hur bör jag tänka/vad gör jag fel/rätt?

Tack på förhand!

Mvh