Beräkna volymen av den rotationskropp som uppstår

Nej det är inte rätt.

Eftersom du integrerar i y-led så ska integrationsgränserna vara 0 och 2, inte 0 och 4.

Du verkar tänka rätt med integranderna, men försök att med ord eller bild beskriva vilka volymer de två integralerna avser.

Är det rätt nu? 

Ja, fast du bör svara med ett exakt värde för att få full poäng.

En av rotationskropparna du volymberäknar har formen av en kon, så den kan enklare volymberäknas med hjälp av formeln $V=\frac{\pi r^2h}{3}$

(32pi/5) = V1 

(32pi/3) =V2 

Ska man då ta (32pi/3)-(32pi/5)=64pi/15 v.e 

1. är det rätt svar nu? 
2. Hur kan du se att det kommer bildas en kon? 

Katarina149 skrev:

(32pi/5) = V1 

(32pi/3) =V2 

Ska man då ta (32pi/3)-(32pi/5)=64pi/15 v.e 

1. är det rätt svar nu? 

Ja

2. Hur kan du se att det kommer bildas en kon? 

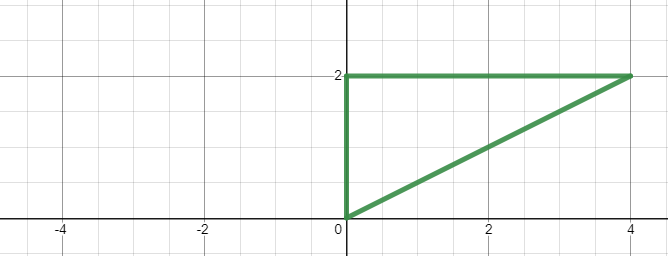
Området som begränsas av linjerna x = 0, y = 2 och y = x/2 bildar en rätvinklig triangel. När den triangeln roterar ett varv runt y-axeln bildas en kon.

Området som begränsas av linjerna x = 0, y = 2 och y = x/2 bildar en rätvinklig triangel. När den triangeln roterar ett varv runt y-axeln bildas en kon.
 

Kan du visa med hjälp av en bild? :)

Området som begränsas av linjerna bildar en rätvinklig triangel:

När området roterar ett varv runt y-axeln bildas en kon:

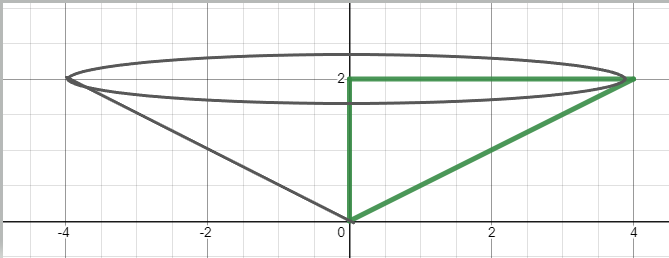
Jaha ok tror att jag förstår nu. Tackar!