Beräkna verkningslinjens skärning med y-axeln
Hej,
Sitter fast på denna uppgift:
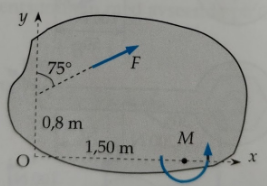
En kropp påverkas av en kraft F = 57 N och ett rent moment M = 46 Nm. Ersätt kraftsystemet med en enda kraft och bestäm var verkningslinjen för denna skär y-axeln.
Jag har komposantuppdelat F och fått fram:
∑Fx=
Om systemet ska reduceras till en enda kraft så måste satisfieras.
Alltså är momentarmen med avseende på O:
Hur går jag vidare för att beräkna var verkningslinjen skär y-axeln?
Tack på förhand!
Hej Aleta och välkommen till pluggakuten,
Jag tror att den som gjort uppgiften har tänkt sig att det dels är en kraft F dels är ett moment som verkar på kroppen. Alltså har vi
Där den sista termen står för kraftparsmomenten (i det här fallet bara M)
När du beräknat det totala momentet kring kan du ersätta det givna kraftsystemet med en kraftresultant som ger precis samma kraftmoment runt origo. Du kan därför ansätta angreppspunkten och lösa ekvationen
Guggle skrev:Hej Aleta och välkommen till pluggakuten,
Jag tror att den som gjort uppgiften har tänkt sig att det dels är en kraft F dels är ett moment som verkar på kroppen. Alltså har vi
Där den sista termen står för kraftparsmomenten (i det här fallet bara M)
När du beräknat det totala momentet kring kan du ersätta det givna kraftsystemet med en kraftresultant som ger precis samma kraftmoment runt origo. Du kan därför ansätta angreppspunkten och lösa ekvationen
Tack så mycket för svar Guggle!
Om jag förstått rätt ska då
och .
Facit säger att den skär vid , men det måste nästan ha med avrundning att göra?
Nja, du har räknat rätt fram till slutet och du har fått rätt , men sen har du glömt att x-komposanten av är eller om du så vill
Alltså får du
Där jag tog med några decimaler extra för att visa var det gått fel.
Jag vet inte om ni räknar med kryssprodukter, men om ni lärt är det är det bättre att du räknar med vektorer och kryssprodukter hela vägen så slipper du slarvfel :)
Guggle skrev:Nja, du har räknat rätt fram till slutet och du har fått rätt , men sen har du glömt att x-komposanten av är eller om du så vill
Alltså får du
Där jag tog med några decimaler extra för att visa var det gått fel.
Jag vet inte om ni räknar med kryssprodukter, men om ni lärt är det är det bättre att du räknar med vektorer och kryssprodukter hela vägen så slipper du slarvfel :)
Ah, tack! Då förstår jag :) Vi använder inte kryssprodukt i fysikkursen, men det sitter nog kvar någorlunda sedan linjär algebra. Så får titta lite närmare på det där!