Beräkna summan av p+q+r+s
Skulle man kunna rita en vinkelrät linje invid vinkel q ?
Eller är p= q+r enligt yttervinkelsatsen ?
Förslag: Inför en hjälpvinkel u enligt bilden.
Försök att hitta ett samband mellan u, r och s samt ett annat samband mellan u, p och Q.

Är u= r+s, enligt yttervinkelsatsen ?
q= r+p ?
Arup skrev:Är u= r+s, enligt yttervinkelsatsen ?
Nej.
Försök att hämta lite inspiration från den här tråden.
Arup skrev:q= r+p ?
Vad är sidovinklarna till samtliga vinklar? Markera dessa och skriv ut vinkel.
Låt sidovinklen till u vara x.
Teckna två uttryck för x. Sedan är du klar.
Trinity 2 hur menar du ? Vilka vinklar skall betecknas m. x ?

Som svar på din tidigare fråga om vinkel u: nej, men enligt yttervinkelsatsen är
u = 180 - r + 180 - s.
Vad får du på motsvarande sätt för x?
Om du har markerat u på det sätt som visas i svar #3 så kan du bara summera vinklar i 2 trianglar. Du kan säkert lista ut vilka trianglar som använts.
Du får ekv1:
180-s + 180-r +180-u = 180
s+r+u=360
och ekv2
180-p +u + 180-q = 180
-p+u-q=-180
p-u+q=180
addera ekv1 och ekv2
Edit: du kan såklart använda yttervinkelsatsen om det känns bättre.
Jag har löst det! Ska dock justera till en tjusigare lösningsförslag
Tack joculator. Men, hur skulle man kunna lösa problemet med yttervinkelsatsen som du nämnde ?
Du har skrivit av dig själv fel, 360 har blivit 180. Svaret är 540o.
Jag föreslog en lösning med yttervinkelsatsen i #9.
Det finns fler sätt, men det är inga stora skillnader mellan några av lösningarna.
Yttervinkelsatsen är en liten genväg ibland, men triangelns vinkelsumma fungerar alltid.
Arup skrev:Trinity 2 hur menar du ? Vilka vinklar skall betecknas m. x ?
Så här
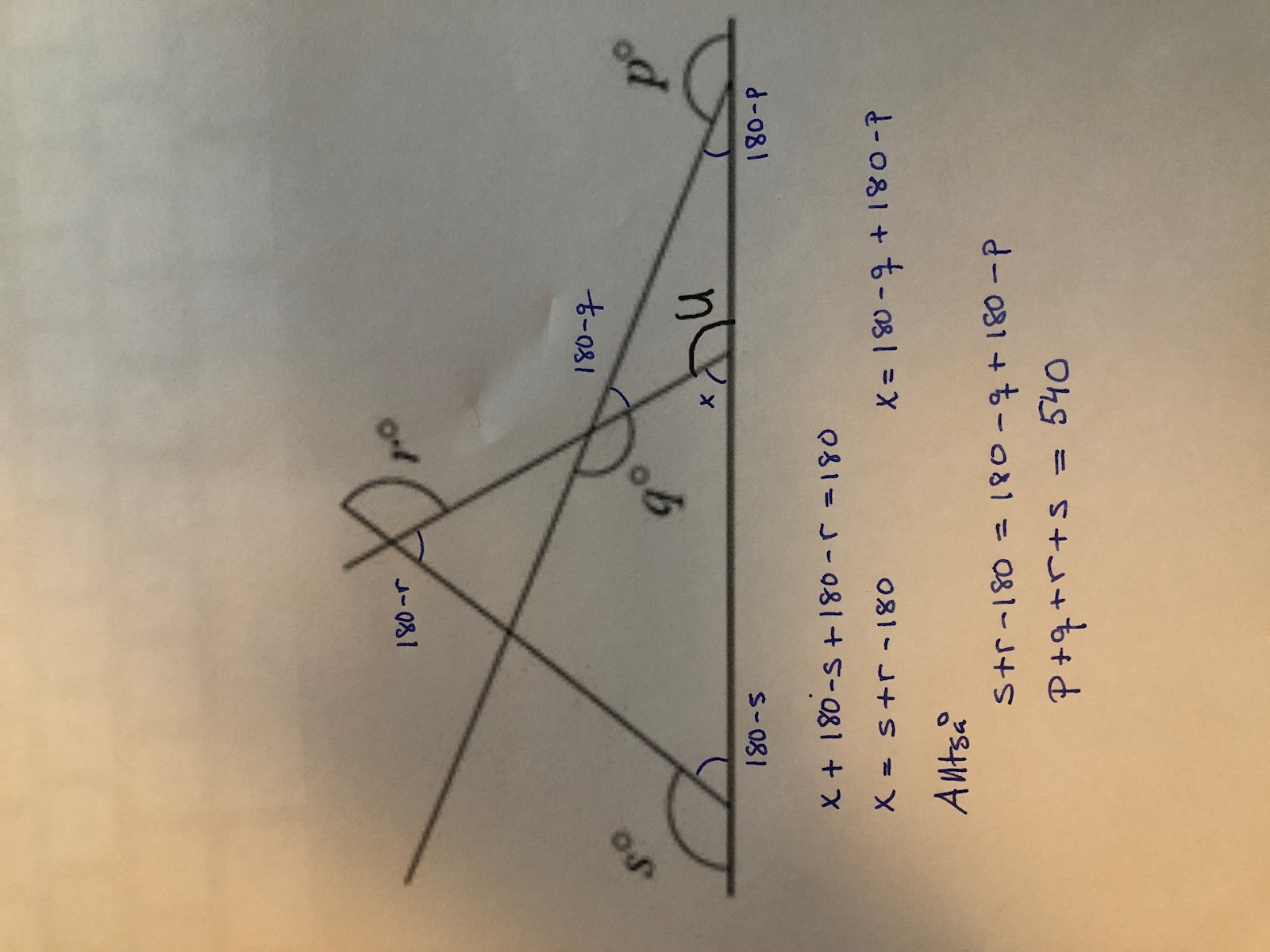
@Trinity2 vad gjorde jag för del då ?
var min uträkning fel med algebran eller var det att jag ställde upp på ett felt sätt ?
Se #13. Du skrev av Joculators lösning, men i sista raden för ekv 1 har du skrivit =180 fast du skrev =360 på raden ovanför. När du rättar och summerar ekvationerna får du = 540.



