Beräkna spänningen
Hej! Till uppgiften nedan har jag räknat ut U i spänningskällan (6.24V). Sedan räknade jag ut ersättningsresistansen till 100, 120 och 220 resistorerna (110 ohm). Spänningen över ersättningsresistansen har jag dessutom fått till 2,64V. Hur går jag nu till väga för att räkna ut hur stor spänningen över resistorn med resistansen 120 Ω är?
Uppgiften:
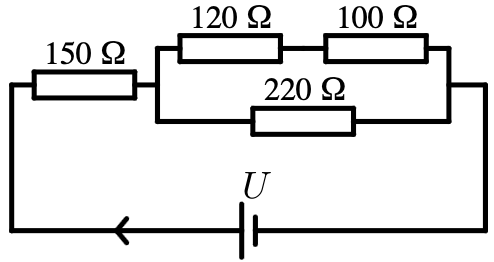
Fyra resistorer är kopplade så som kopplingsschemat visar. Med en voltmeter mäts spänningen över resistorn med resistansen 150 Ω till 3,6 V.
- Hur stor är den pålagda spänningen U? (FICK RÄTT SVAR: 6,24V)
- Hur stor är spänningen över resistorn med resistansen 120 Ω?
Hej!
Om du vill fortsätta på det spåret som du redan börjat på.
- Du vet att spänningen över 120ohm med 100 ohm is serie är 2.64V. Hur fördelar sig den spänningen över dessa två motstånd.
Annars hade du också kunnat utgå ifrån strömmen. Strömmen genom 150Ohm måste fördela sig på de två paralellkopplade benen. Hur fördelar sig strömmen i dessa benen? Och hur stor blir då spänningen över 120ohm nör du vet strömmen genom den?
Kommer du vidare?
Spänningen jag fått till 2.64V är för ersättningsresistansen 120 ohm, 100 ohm och 220 ohm. Jag vet att spänningen över resistorerna 120 och 100 ohm (tillsammans 220 ohm) är parallellkopplade med 220 ohm resistorn. Då har vi 2 parallellkopplade grenar. Hur kan jag veta hur spänningen kommer fördela sig mellan dem om jag inte heller vet hur strömmen fördelar sig mellan dem?
Du har kommit såhär långt, eller hur?
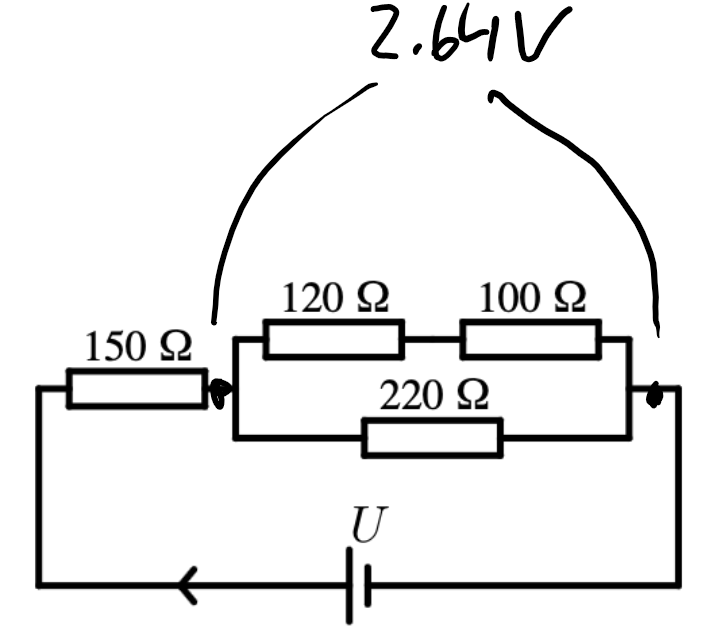
Det betyder att spänningen över 220ohmsmotståndet är 2.64V. Det betyder _också_ att spänningen över 120ohm+100ohm är 2.64V (eftersom spänningen över två paralellkopplade motstånd måste vara lika). Du kan alltså fortsätta resonera kring hur spänningen 2.64V fördelar sig på 120+100ohm, utan att behöva bry dig om 220ohmsmotståndet.
Hänger du med?
Hänger med! Men strömmen som går genom 150 ohm's resistorn är densamma som går igenom alla tre resistorerna, eftersom det endast blir en seriekoppling om alla inkluderas i ersättningsresistansen ju? Tror jag missar något 😅
Men jag hänger med i ditt resonemang! Har nu fått strömmen som flödar genom övre grenen (0.012A) och m.h.a det räknat ut att spänningen över den önskade resistorn är 1.44V. Är dock fortfarande intresserad av att veta svaret till frågan ovan.
Hänger med! Men strömmen som går genom 150 ohm's resistorn är densamma som går igenom alla tre resistorerna, eftersom det endast blir en seriekoppling om alla inkluderas i ersättningsresistansen ju? Tror jag missar något 😅
Du har räknat ut att strömmen genom 150ohmaren är 3.6/150=24mA. Det är samma ström som går igenom ersättningsresistansen av de tre andra motstånden. Så långt hänger du med tror jag, eller hur?
Men genom att räkna ut ersättningsresistansen av de tre serie/paralellkopplade motstånden så "tappar du bort" informationen om hur stor ström som går genom vardera benet i paralellkopplingen. Strömmen 24mA delar ju på sig, så att en del av 24mA går genom övre benet, och resterande går genom undre benet. Du måste alltså ta ett steg tillbaka för att se hur dessa 24mA delar på sig.
(För om du hade fortsatt det felaktiga resonemanget att 24mA flyter genom alla tre motstånden, så hade ju inte strömmen "räckt till". Eller hur?)
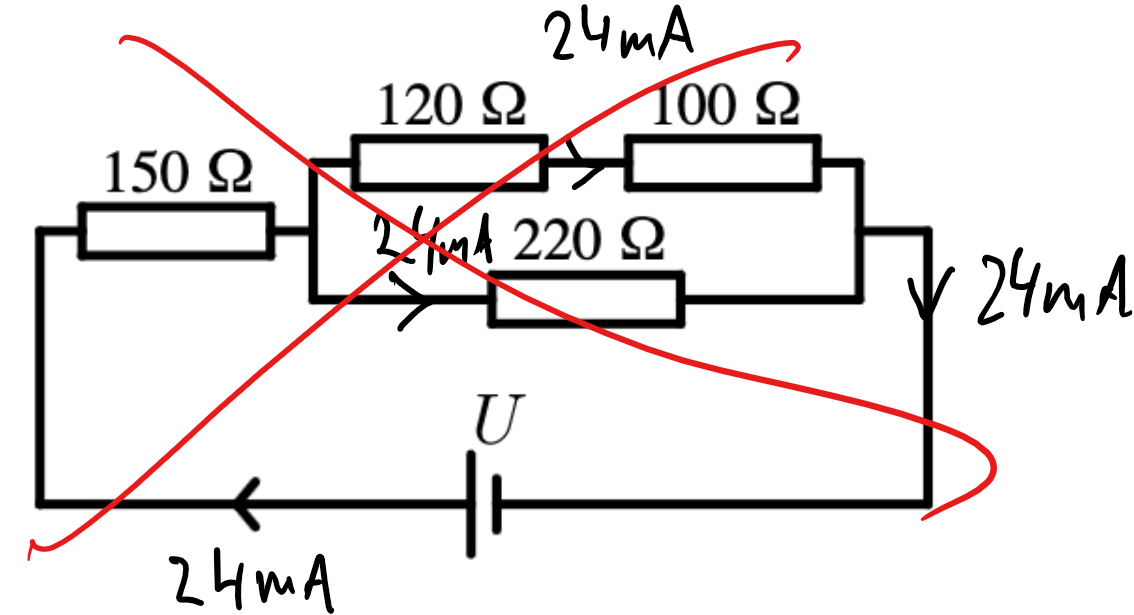
Yes! Alltså blir det helt enkelt såhär: Strömmen som går igenom resistor 150 är densamma som går igenom de övriga 3 resistorerna tillsammans (ersättningsrrsistansen). Med hjälp av detta kan jag ta reda på spänningen över hela parallellkopplingen, som förblir densamma för varje gren eftersom grenarna har lika stor resistans. Efteråt kan jag ta reda på strömmen som går igenom övre förgreningen och därmed räkna ut spänningen över resistor 120. Har jag förstått rätt? 🙌🏼
Hade detta fortfarande gällt ifall grenarna hade olika stor resistans? T.ex. 100 ohm i den övre, och 50 i den nedre?
Hade detta fortfarande gällt ifall grenarna hade olika stor resistans? T.ex. 100 ohm i den övre, och 50 i den nedre?
Vad skönt att du lade till den är frågan! Jag höll på att skriva att spänningsfallet över två parallellkopplade grenar är _alltid_ lika stort, oavsett resistansen i respektive gren. Det är strömdelningen per gren som fixar detta. Dvs om resistansen i en gren är lägre, så går det istället högre ström genom den så att spänningsfallet i grenarna blir lika.
Det vore fysikaliskt omöjligt att ha olika spänningsfall i parallellkopplade grenar, för då skulle man ju på något sätt kunna få olika värde på spänningspotentialen i en och samma punkt, och det skulle ju omedelbart justeras av laddningarna (strömmarna).
Tack så mycket för din hjälp!



