Beräkna spänning med spänningsdelning

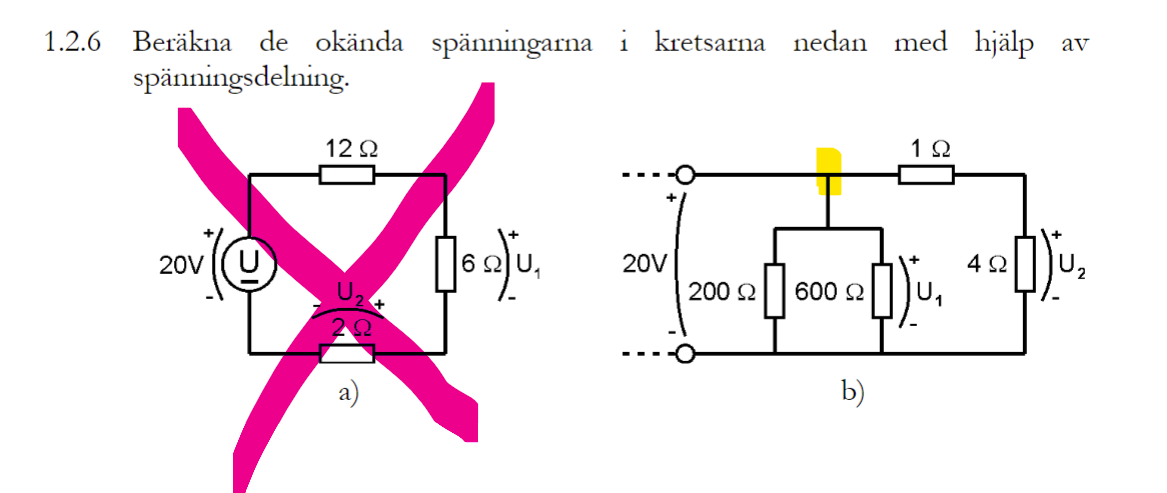
Spänningen delas, så den blir mindre än 20 volt.

(Eller inte. För U₁ behöver du inte räkna alls.)

Jag har sett att spänningen ska bli 20v för U1 som du säger, är detta för att strömmen kan gå ett varv och då endast gå genom resistansen på 600ohm? Efter att ha sett vad svaret ska bli och testat olika sätt med siffrorna får jag rätt svar med dessa beräkningarna. Är det korrekta beräkningar? Varför blir det 1/200 på U1 och inte 200? Är det för att de är parallellkopplade?

Aorta skrev:

Är det för att de är parallellkopplade?

Ja. 

Precis som eluttagen i en sladdosa är parallellkopplade. Alla är 230 volt.

Så för att räkna U₂ behöver du bara tänka på att det står 20 volt över 1 Ω i serie med 4 Ω. Det går med huvudräkning.

Okej, då tror jag att jag förstår! Tack!

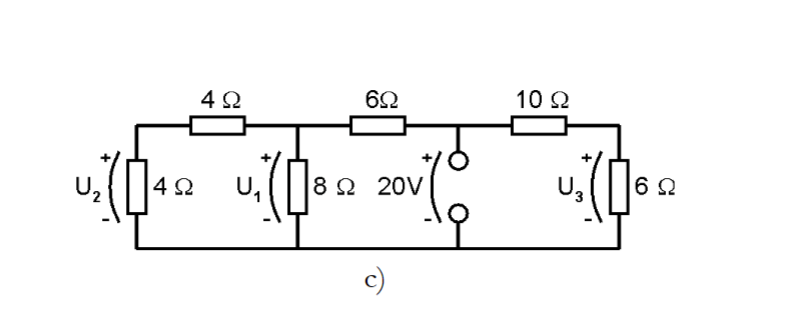
Jag har gått vidare till uppgift c) men stöter på patrull även där. U3 får jag rätt på men ej på U1 och U2. Jag har kollat en väg i taget och använt formeln för spänningsdelning. Behöver jag göra något särskilt med resistansen på 6ohm då den ingår i både vägen för U1 och U2?

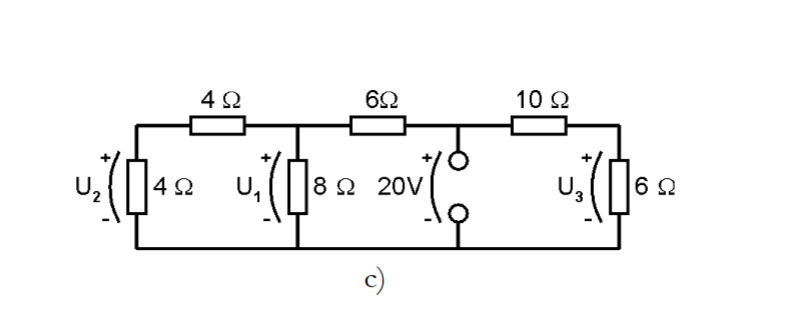
Aorta skrev:

... använt formeln för spänningsdelning...

Ser du inte genom att bara titta att U₂ är hälften av U₁ ?

Och att det är snälla värden, så att det totala motståndet av den vänstra kretsen är 10 Ω?

Nej, det kan jag inte se direkt men förstår det när jag ställer upp ekvationerna. Värdena jag fick fram är U2 hälften av U1 men jag har fått fel värden. U1 ska vara 8V och U2 4V. Hur blir det totala motståndet 10ohm på den vänstra (gulmarkerade) kretsen? Blir det inte 14? 4+4+6. 

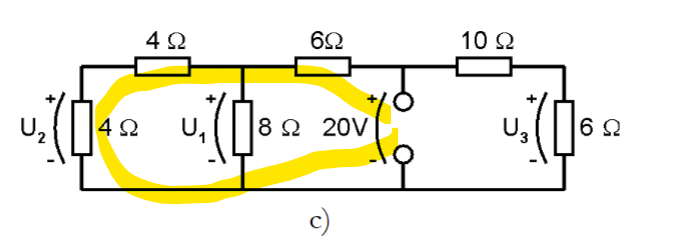
Aorta skrev:

Hur blir det totala motståndet 10ohm  

6 Ω i serie med 8 //(4+4) Ω.

Jag hänger fortfarande inte med helt. Jag förstår nu att motståndet blir 10ohm i nämnaren men får mina svar till U1=16V och U2=8V, båda är alltså dubbelt så stora som de ska vara. Har jag tänkt fel i dessa beräkningarna?

Aorta skrev:

Jag hänger fortfarande inte med helt. Jag förstår nu att motståndet blir 10ohm i nämnaren men får mina svar till U1=16V och U2=8V, båda är alltså dubbelt så stora som de ska vara. Har jag tänkt fel i dessa beräkningarna?

Hur stor spänning får du då över 6-Ω-motståndet undrar jag.

För att bestämma U₁ blir det 4 Ω i täljaren, eftersom ersättningsmotståndet är $R_{\rm par} = 4 \ \Omega$ i serie med 6 Ω.

Spänningsdelningen är så att det står $\frac{6}{6+4}\times 20 = 12$ volt över 6-Ω-motståndet och $\frac{4}{6+4}\times 20 = 8$ volt över parallellkopplingen.

U3 får jag till 7,5V vilket ska vara korrekt. 

Jag förstår att ersättningsmotståndet över parallellkopplingen är 4ohm. Men spänningarna över U1 och U2 blir olika. Om jag ska använda 4 ohm (ersättningsmotståndet för parallellkopplingen) till U1, varför ska jag inte använda samma till U2? När jag kollar på den tycker jag att det ser lika "jobbigt" ut för strömmen att at vilket som av hållen då resistansen på de två olika vägarna är lika stora.

Om spänningen över resistansen 6 ohm är 12V och U1=8v och U2=12-8=4V. Men om jag skulle räknat ut U2 för sig själv istället så hade jag fått fram 8v för den, då ersättninsmotståndet är 4v och den är i serie med 6v - uträkningen blir då likadan som för U1.

Jag förstår alltså inte varför det går att använda ersättningsmotståndet i täljaren för att beräkna U1 då det för mig inte verkar som att jag skulle kunna göra samma för U2.

Aorta skrev:

U3 får jag till 7,5V vilket ska vara korrekt. 

Jag förstår att ersättningsmotståndet över parallellkopplingen är 4ohm. Men spänningarna över U1 och U2 blir olika. Om jag ska använda 4 ohm (ersättningsmotståndet för parallellkopplingen) till U1, varför ska jag inte använda samma till U2? När jag kollar på den tycker jag att det ser lika "jobbigt" ut för strömmen att at vilket som av hållen då resistansen på de två olika vägarna är lika stora.

Om spänningen över resistansen 6 ohm är 12V och U1=8v och U2=12-8=4V. Men om jag skulle räknat ut U2 för sig själv istället så hade jag fått fram 8v för den, då ersättninsmotståndet är 4v och den är i serie med 6v - uträkningen blir då likadan som för U1.

Jag förstår alltså inte varför det går att använda ersättningsmotståndet i täljaren för att beräkna U1 då det för mig inte verkar som att jag skulle kunna göra samma för U2.

Det förvånar mig att du inte omedelbart ser att U₂ är halvt så stor som U₁.

Du behöver inte göra det med spänningsdelning. Det kan vara en bra idé att räkna ut alla strömmar och alla spänningar med endast Ohms lag och Kirchhoffs lagar och att lösa uppgiften på det sättet.

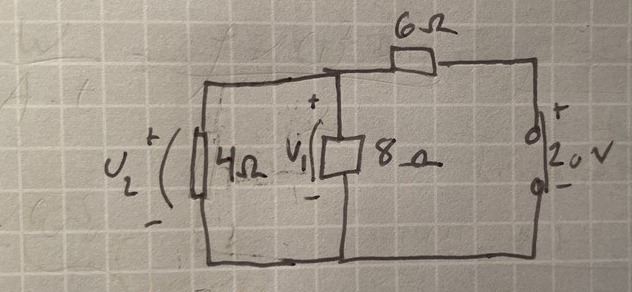
Om det hade sett ut såhär hade jag varit med på det direkt. Men den andra resistansen på 4ohm gör mig förvirrad. Jag jag tänkt att det i täljaren ska vara resistansen på det stället som en räknat på, alltså 8 för U1 och 4 för U2. Jag hade varit med på att nämnaren blir samma för båda.

Om jag ska ha 4 i nämnaren för U1, ska jag då ha 2 i nämnaren för U2?

Aorta skrev:

Om det hade sett ut såhär hade jag varit med på det direkt.

Hade du? Hur tycker du att det blir då?

Jag tycker det blir såhär

Okej, jag får testa det istället. Tack

Nej.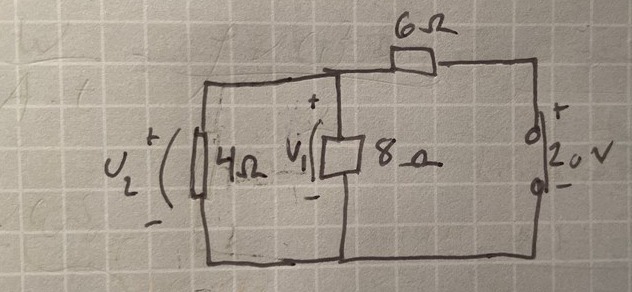
Vad har du då för spänning över 6 Ω där? Vad har du för strömmar?

Kolla om dina värden stämmer med Ohms lag, med Kirchhoffs lagar.