Beräkna sannilikheten P(max(zeta,eta)>0,7)
Hej! Jag förstår inte riktigt hur de gjort i facit. Har de inte skrivit fel på vissa saker? Om jag kopierar facit och ändrar så som jag tänker att det ska vara. Menar de inte:
Vi söker P(max(ζ, η) > 0.7).
Vi har P(max(ζ, η) > 0.7) = 1 − P(max(ζ, η) ≤ 0.7) = 1 − P(ζ ≤ 0.7, η ≤ 0.7).
Att ξ1, . . . , ξ4 medför att ζ, η är oberoende. Så:
P(max(ζ, η) > 0.7) = 1 − P(ζ ≤ 0.7) · P(η ≤ 0.7).
****Ändring på raden nedan: P(ξ3 > 0.7, ξ4 > 0.7) istället för P(ξ3 > 0.7, ξ4 ≤ 0.7)?***
Vi har P(η ≤ 0.7) = 1 − P(η > 0.7)= 1 − P(ξ3 > 0.7, ξ4 ≤ 0.7) = 1 − P(ξ3 > 0.7) · P(ξ4>0.7) = 1 −
***Ändring på raden nedan: P(ξ1 ≤ 0.7, ξ2 ≤ 0.7) istället för P(ζ ≤ 0.7, η ≤ 0.7)?***
Vi har P(ξ1 ≤ 0.7, ξ2 ≤ 0.7) = P(ξ1≤ 0.7)P(ξ2≤ 0.7) =
Så P(max(ζ, η) > 0.7) = 1 − · (1 − ) = 0.5541.
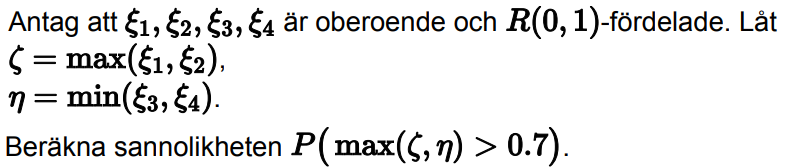
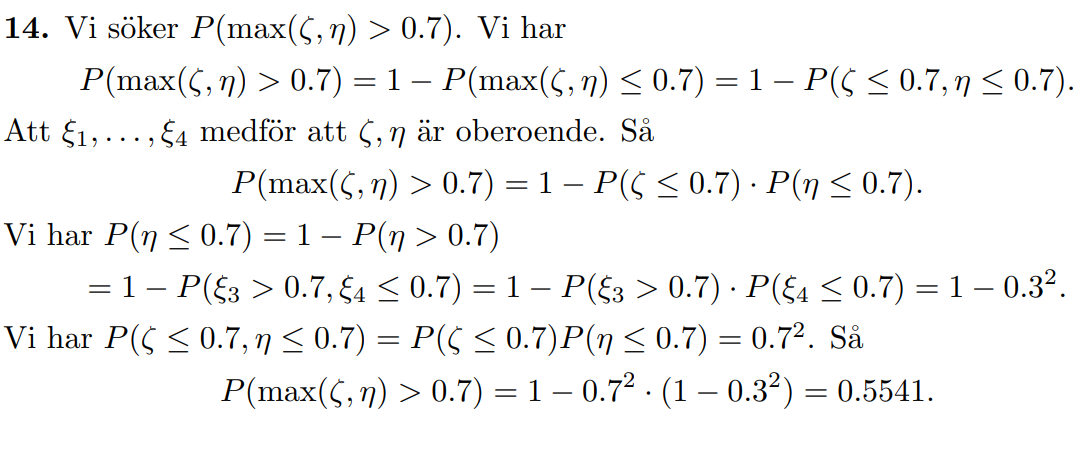
Tack på förhand!
Korrekt korrigeringar, klantigt av facit.
Aldrig stött på notationen R(0,1) tidigare, syftar de på uniform-fördelningen?
Calle_K skrev:Korrekt korrigeringar, klantigt av facit.
Okej vilken tur tack så mycket! Har dock en följdfråga, jag förstår inte riktigt varför i så fall man tar 1 - för ξ3 och ξ4 men man tar inte det för ξ1 & ξ2?
Calle_K skrev:Aldrig stött på notationen R(0,1) tidigare, syftar de på uniform-fördelningen?
Jag tror de menar rektangelfördelning i intervall (0,1)?
Hejhej! skrev:Calle_K skrev:Korrekt korrigeringar, klantigt av facit.
Okej vilken tur tack så mycket! Har dock en följdfråga, jag förstår inte riktigt varför i så fall man tar 1 - för ξ3 och ξ4 men man tar inte det för ξ1 & ξ2?
Vi sätter 1- framför index 3 och 4 för att få <= istället för >=
Calle_K skrev:Hejhej! skrev:Calle_K skrev:Korrekt korrigeringar, klantigt av facit.
Okej vilken tur tack så mycket! Har dock en följdfråga, jag förstår inte riktigt varför i så fall man tar 1 - för ξ3 och ξ4 men man tar inte det för ξ1 & ξ2?
Vi sätter 1- framför index 3 och 4 för att få <= istället för >=
Ah okej tack! Men är det för att ξ1 & ξ2 är minimi?
Precis


