Beräkna resistans på metallslinga

Har en uppgift som lyder följande: En slinga av en ledande tråd ligger platt på ett bord i form av en kvadrat med sidan 5,0dm.

Under loppet av 3,0ms formas tråden om till en rektangel med kortsidan 1,0 dm, men med samma omkrets som innan.

I rummet där slingan befinner sig är den jordmagnetiska flödestätheten 53μT med inklinationsvinkeln 71°.Under denna process induceras en ström i slingan med medelvärdet 64mA.

Bestäm slingans resistans.

Det jag samlar ihop från uppgiften är detta:

Ks₁(Kortsida på första kvadraten) = 0,5m

Ks₂(Kortsida på rektangeln efter slingan har tryckts ihop) = 0,1m

t = 0,003 s

B = $53\times {10}^{-6} T$

i = 71 grader

I = 64 mA = 0,064 A

Börjar med att dela upp jordmagnetiska flödestätheten i sina komposanter B_v och B_h, eftersom slingan ligger platt på ett bord och det måste vara vinkelrät för att inducera någon spänning så tänker jag att B_v är den intressanta komposanten. 

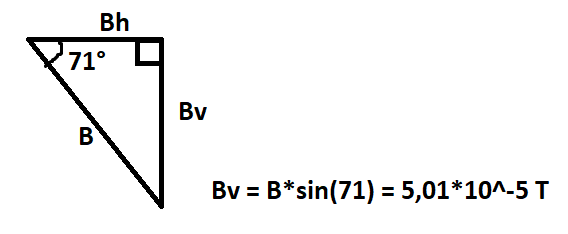
Får då fram att B_v=$5,01*{10}^{-5} T$. Tänker att jag skall använda e=VBL för att få fram den inducerade spänningen. 

Har då första kortsidan Ks₁ = 0,5m och Ks₂ = 0,1m, eftersom omkretsen är samma för båda figurerna så räknas nya långsidan ut via O₁=0,5*4=2 => O₂=2=(0,1*2) + (2Ls) => Ls = (2-0,2)/2 = 0,9m

Alltså är nya långsidan 0,9m och nya kortsidan är 0,1m

Sedan för hastigheten så skedde denna förändring i form, från 0,5-0,1=0,4m på 3ms, räknar då V=s/t=0,4/0,003 = 133,33... m/s

Använder sedan e=VBL=133,33*(5,01*10-5)*0,9=0,006 V

Sedan till sist U=RI => R=U/I = 0,006/0,064 = 0,0939 ohm. Det är fel då svaret skall vara 41,8 ohm.

Blev en lång förklaring så skriv om någon behöver förtydligas, tacksam för hjälp! :)