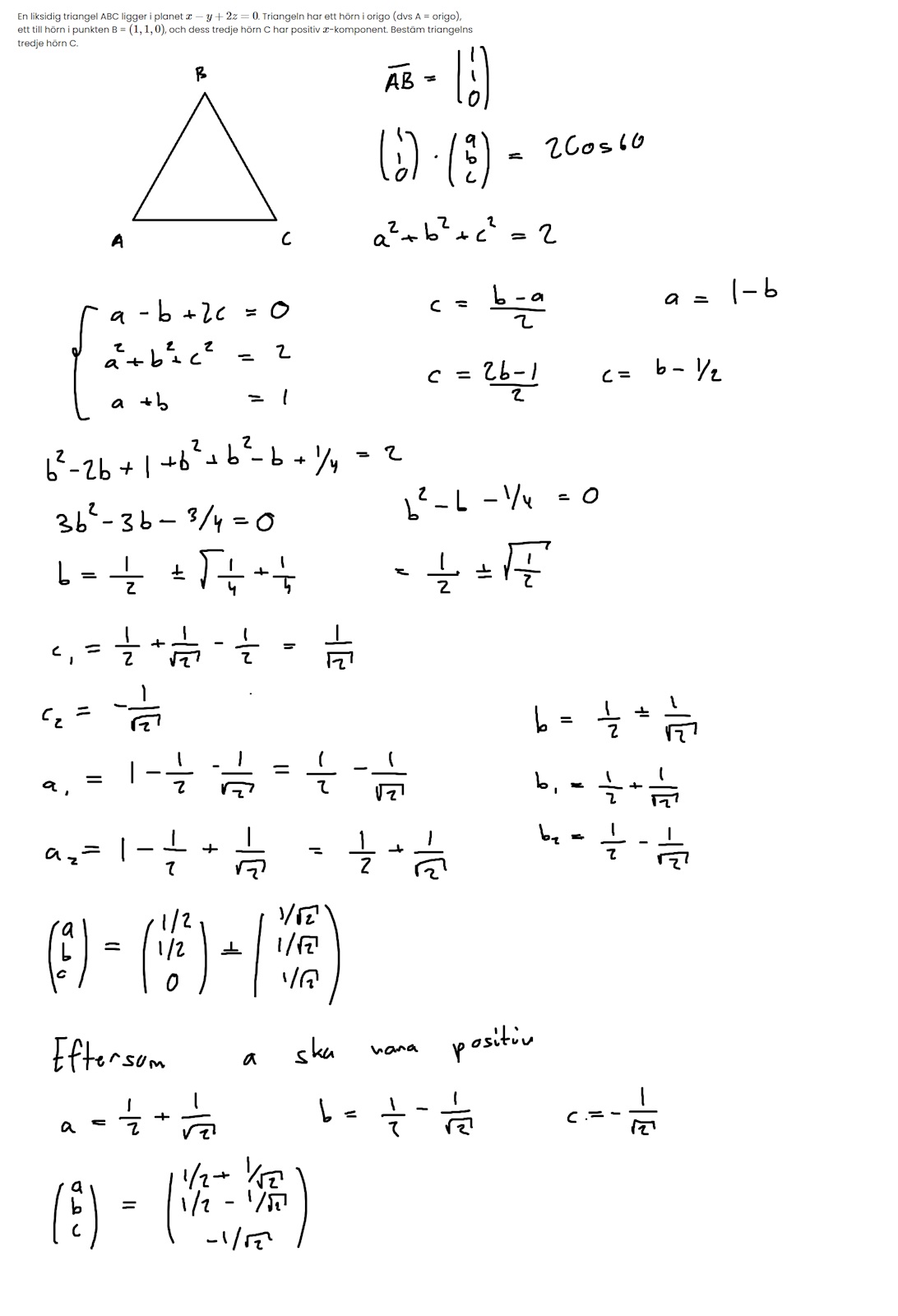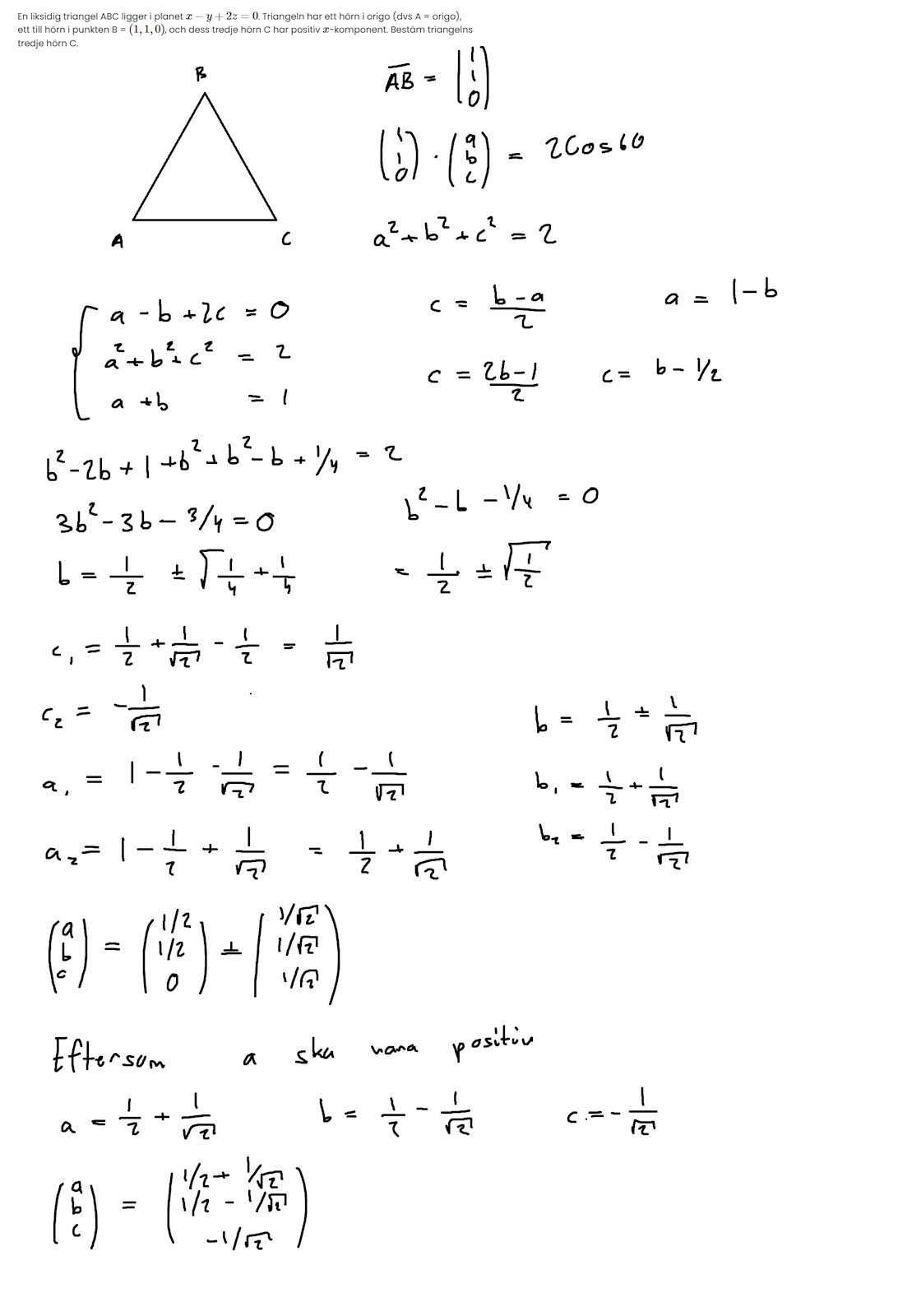beräkna punkt för liksidig triangel i plan
Frågan lyder:
En liksidig triangel ABC ligger i planet . Triangeln har ett hörn i origo (dvs A = origo),
ett till hörn i punkten B = , och dess tredje hörn C har positiv -komponent. Bestäm triangelns
tredje hörn C.
Jag gjorde först en lista på saker frågan förklarade
- Punkt A,B och C måste ligga på planet
- C i positiv x riktning
- liksidig triangel, alla hörn samma vinkel och samma norm
Jag skrev om punkten C som = och använde formeln då jag visste normen, längden och behövde punkten C.
Jag utförde beräkningarna och visste att jag använt väldigt fel metod för att lösa ut C då jag fick ett orimligt ekvationssystem
Vilken metod är det man ska använda för att lösa frågan?
Följer. Är på samma problem.
Vi hade liknande problem tidigare.
PATENTERAMERA skrev:Vi hade liknande problem tidigare.
Hej,
Jag lyckades lösa den ganska väl med din metod nu när jag körde med den. Det som gör mig lite orolig är lösningsförslaget som föreslog att man skulle hitta en vektor som är ortogonal mot normalen och som är vinkelrät AB vektorn. Examinatorna kan ibland vara petiga så jag undrar om det är okej att lösa frågan på detta sätt.
WimpyBaby skrev:Frågan lyder:
En liksidig triangel ABC ligger i planet . Triangeln har ett hörn i origo (dvs A = origo),
ett till hörn i punkten B = , och dess tredje hörn C har positiv -komponent. Bestäm triangelns
tredje hörn C.
Jag gjorde först en lista på saker frågan förklarade
- Punkt A,B och C måste ligga på planet
- C i positiv x riktning
- liksidig triangel, alla hörn samma vinkel och samma norm
Jag skrev om punkten C som = och använde formeln då jag visste normen, längden och behövde punkten C.
Jag utförde beräkningarna och visste att jag använt väldigt fel metod för att lösa ut C då jag fick ett orimligt ekvationssystem
Vilken metod är det man ska använda för att lösa frågan?
Lösningen jag kom fram med ifall någon där i framtiden behöver den :)
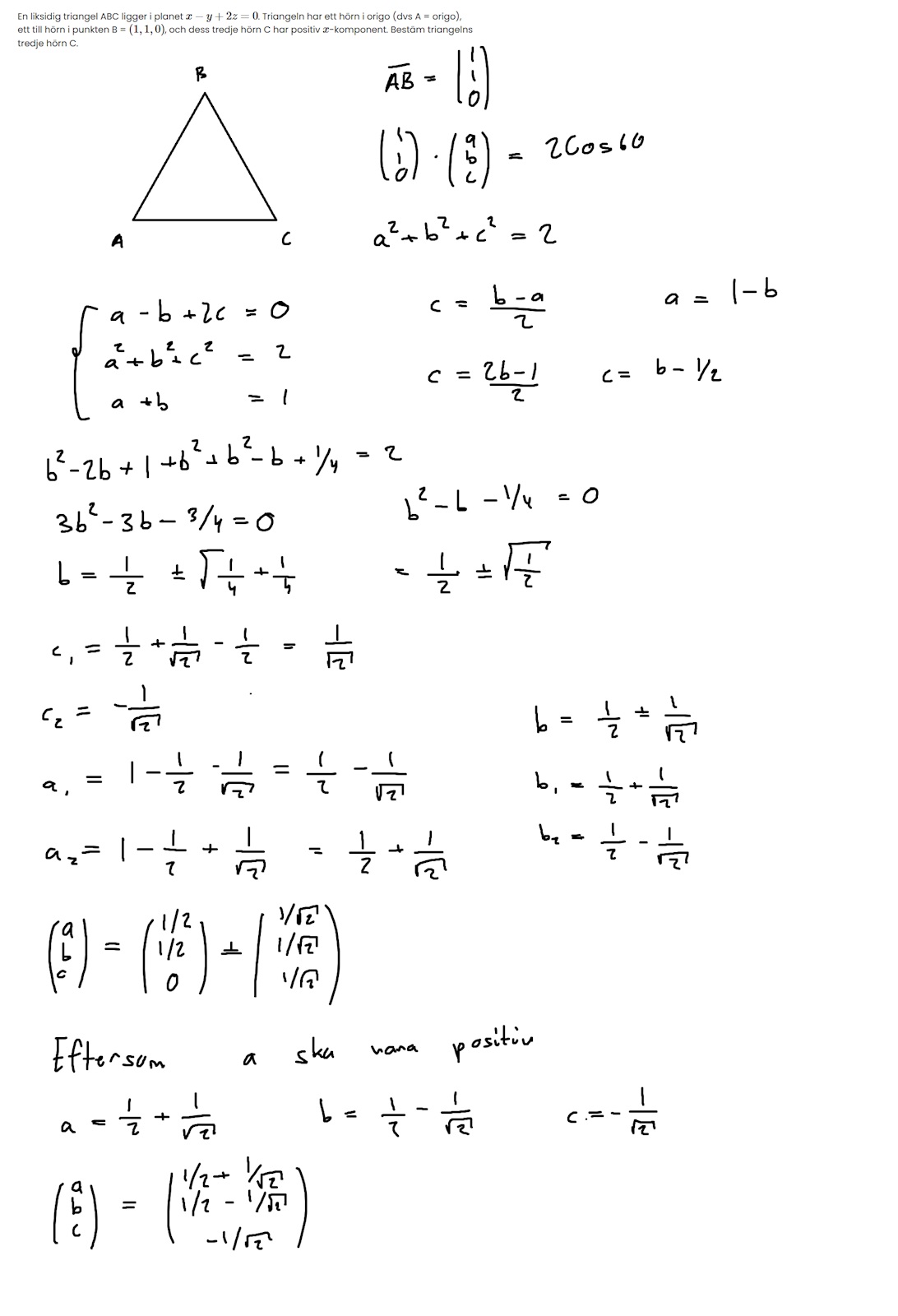
WimpyBaby skrev:PATENTERAMERA skrev:Vi hade liknande problem tidigare.
Hej,
Jag lyckades lösa den ganska väl med din metod nu när jag körde med den. Det som gör mig lite orolig är lösningsförslaget som föreslog att man skulle hitta en vektor som är ortogonal mot normalen och som är vinkelrät AB vektorn. Examinatorna kan ibland vara petiga så jag undrar om det är okej att lösa frågan på detta sätt.
Det tror jag skulle vara OK. Detta verkar vara en uppgift i linjär algebra och båda lösningarna utnyttjar koncept från linjär algebra. Man kan ju inte kräva att tentanden skall vara tankeläsare och inse precis vilken lösning som facit tänker sig. Dessutom skulle man ju kunna misstänka fusk om alla hade svarat precis med den lösning som facit anger.
WimpyBaby skrev:WimpyBaby skrev:Frågan lyder:
En liksidig triangel ABC ligger i planet . Triangeln har ett hörn i origo (dvs A = origo),
ett till hörn i punkten B = , och dess tredje hörn C har positiv -komponent. Bestäm triangelns
tredje hörn C.
Jag gjorde först en lista på saker frågan förklarade
- Punkt A,B och C måste ligga på planet
- C i positiv x riktning
- liksidig triangel, alla hörn samma vinkel och samma norm
Jag skrev om punkten C som = och använde formeln då jag visste normen, längden och behövde punkten C.
Jag utförde beräkningarna och visste att jag använt väldigt fel metod för att lösa ut C då jag fick ett orimligt ekvationssystem
Vilken metod är det man ska använda för att lösa frågan?
Lösningen jag kom fram med ifall någon där i framtiden behöver den :)
Var kmr a-2b+c som du sätter lika med 0 i ekvation (1) ifrån? och varför kvadrerar du a+b+c och sedan sätter lika med 2 ?
destiny99 skrev:WimpyBaby skrev:WimpyBaby skrev:Frågan lyder:
En liksidig triangel ABC ligger i planet . Triangeln har ett hörn i origo (dvs A = origo),
ett till hörn i punkten B = , och dess tredje hörn C har positiv -komponent. Bestäm triangelns
tredje hörn C.
Jag gjorde först en lista på saker frågan förklarade
- Punkt A,B och C måste ligga på planet
- C i positiv x riktning
- liksidig triangel, alla hörn samma vinkel och samma norm
Jag skrev om punkten C som = och använde formeln då jag visste normen, längden och behövde punkten C.
Jag utförde beräkningarna och visste att jag använt väldigt fel metod för att lösa ut C då jag fick ett orimligt ekvationssystem
Vilken metod är det man ska använda för att lösa frågan?
Lösningen jag kom fram med ifall någon där i framtiden behöver den :)
Var kmr a-2b+c som du sätter lika med 0 i ekvation (1) ifrån? och varför kvadrerar du a+b+c och sedan sätter lika med 2 ?
det är ju planets ekvation. Du vet att punkten C måste befinna i planet, alltså att med värdena i punkten c måste ekvationen för planet stämma. Du vet dessutom att vilket är normen för vektorn mellan A och C. Detta kan du skriva om som då du kvadrerar i båda leden