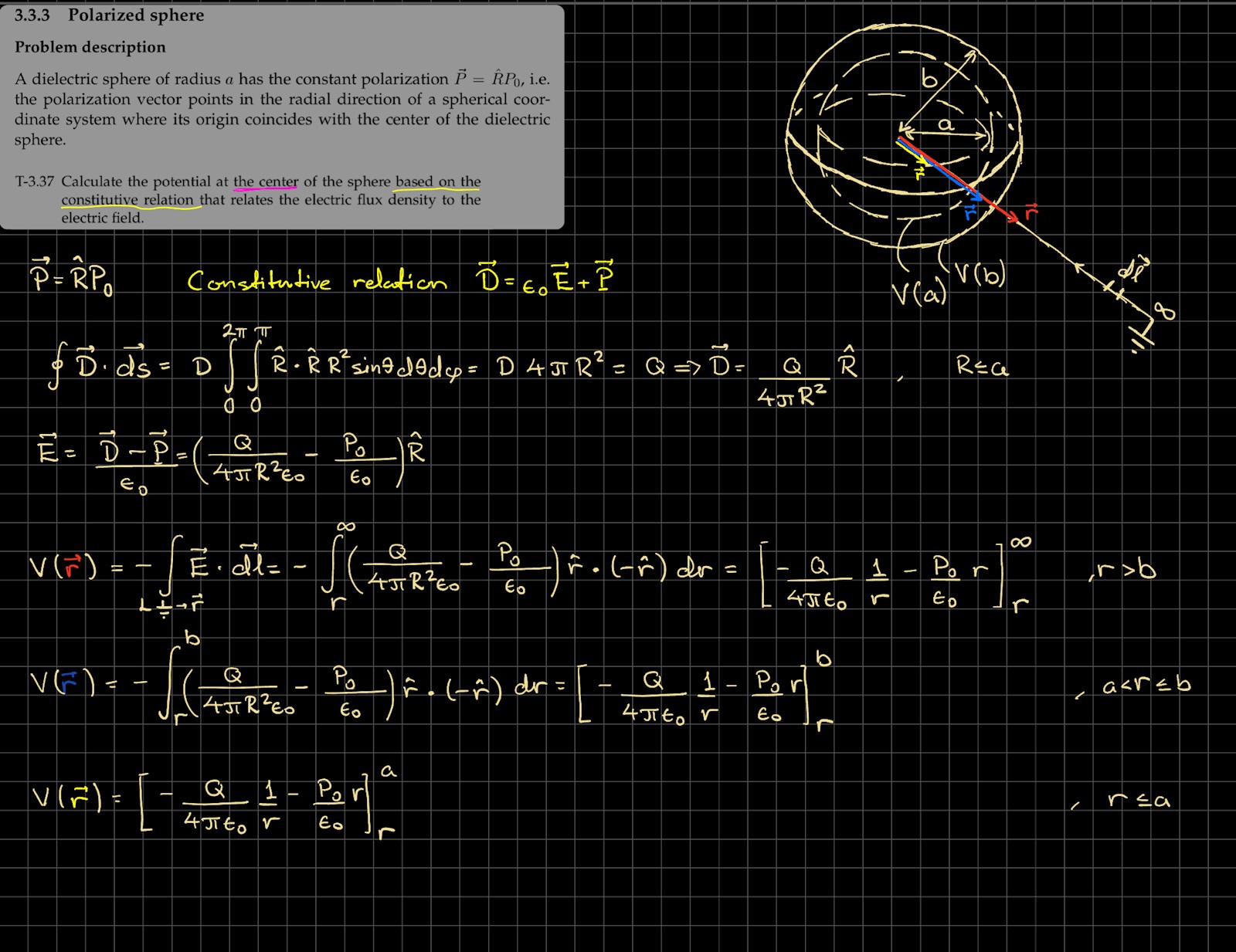
Beräkna potentialen baserat på constitutive relation

Maxwell säger väl att divD = ${\rho }_{fri}$. I ett dielektriskt material så finns det väl ingen fri laddning så divD = 0. Vilket ger att divE = -divP/${\epsilon }_0$.

Pga av symmetri så borde E bara ha en radiell komponent E_r.

E_r(R)$·4\pi R^2$=$\underset{r=R}{∯} \mathit{E}\bullet d\mathit{S}\mathbf{=}\underset{r\le R}{\iiint }div\mathit{E}dV=\frac{-1}{{\epsilon }_0}\underset{r\le R}{\iiint }div\mathit{P}dV=\frac{-1}{{\epsilon }_0}\underset{r=R}{∯} \mathit{P}\bullet d\mathit{S}\mathbf{=}\frac{-P_0}{{\epsilon }_0}·4\pi R^2$.

PATENTERAMERA skrev:

Maxwell säger väl att divD = ${\rho }_{fri}$. I ett dielektriskt material så finns det väl ingen fri laddning så divD = 0. Vilket ger att divE = -divP/${\epsilon }_0$.

Pga av symmetri så borde E bara ha en radiell komponent E_r.

E_r(R)$·4\pi R^2$=$\underset{r=R}{∯} \mathit{E}\bullet d\mathit{S}\mathbf{=}\underset{r\le R}{\iiint }div\mathit{E}dV=\frac{-1}{{\epsilon }_0}\underset{r\le R}{\iiint }div\mathit{P}dV=\frac{-1}{{\epsilon }_0}\underset{r=R}{∯} \mathit{P}\bullet d\mathit{S}\mathbf{=}\frac{-P_0}{{\epsilon }_0}·4\pi R^2$.

Tack så mycket!!

PATENTERAMERA skrev:

Maxwell säger väl att divD = ${\rho }_{fri}$. I ett dielektriskt material så finns det väl ingen fri laddning så divD = 0. Vilket ger att divE = -divP/${\epsilon }_0$.

Pga av symmetri så borde E bara ha en radiell komponent E_r.

E_r(R)$·4\pi R^2$=$\underset{r=R}{∯} \mathit{E}\bullet d\mathit{S}\mathbf{=}\underset{r\le R}{\iiint }div\mathit{E}dV=\frac{-1}{{\epsilon }_0}\underset{r\le R}{\iiint }div\mathit{P}dV=\frac{-1}{{\epsilon }_0}\underset{r=R}{∯} \mathit{P}\bullet d\mathit{S}\mathbf{=}\frac{-P_0}{{\epsilon }_0}·4\pi R^2$.

Jag kom fram till rätt svar för potentialen vid centrum r=0. Om du kan skumma igenom min lösning hade jag uppskattat det som attans!

Min plan var följande, jag löser ut E ur constitutive relation då jag vet att potentialen beror på E. Sen tar jag fram D med hjälp av Gauss. Sen använder jag mig helt enkelt av definitionen för att ta fram potentialen för r=0.