Beräkna p(xi1+xi2>1)
Hej! Jag undrar varför de i facit får att sigma = sqrt(3)? borde inte sigma = sqrt(2) då sigma1 = 1 och sigma2=1 vilket medför att v(xi1)=sqrt(sigma1) = 1, v(xi2) = sqrt(sigma2) = 1 vilket ger:
sigma= sqrt(v(xi)) = sqrt(v(xi1+xi2)) = sqrt(v(xi1) + v(xi2)) = sqrt(1+1) = sqrt(2)?

Facit:

Min lösning:

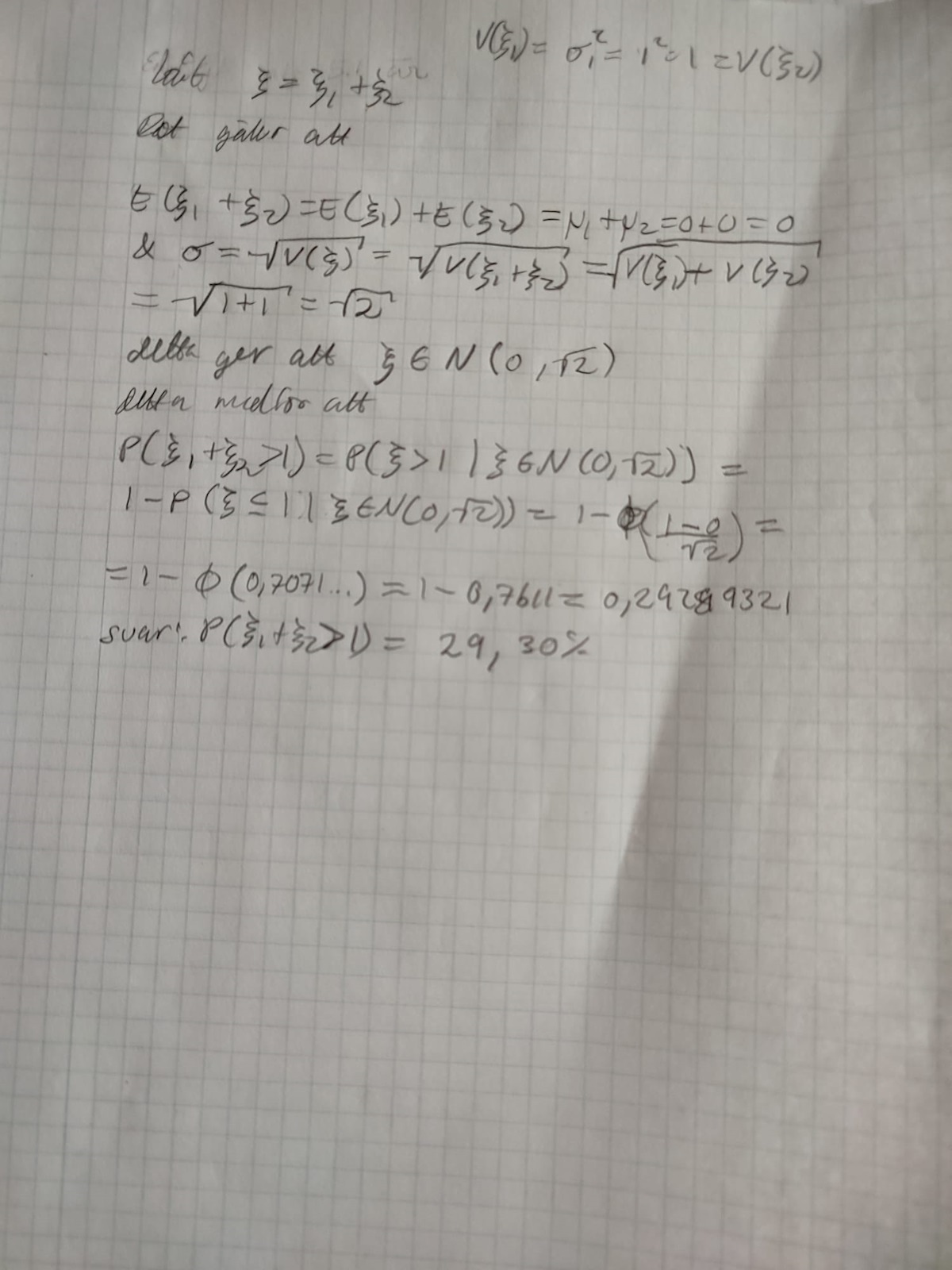
Tack på förhand!
v(ξ1+ξ2)≠v(ξ2)+v(ξ2)
eftersom att de inte är oberoende.
Calle_K skrev:v(ξ1+ξ2)≠v(ξ2)+v(ξ2)
eftersom att de inte är oberoende.
Tack nu förstår jag hur de kommit fram till sigma = sqrt(3), dock vet jag nu då inte hur de bestämmer väntevärdet då xi1 och x2 inte är oberoende?
Väntevärdet är en linjär operator, så det gäller att E[x+y] = E[x] + E[y] oavsett om x och y är oberoende eller inte.
Calle_K skrev:Väntevärdet är en linjär operator, så det gäller att E[x+y] = E[x] + E[y] oavsett om x och y är oberoende eller inte.
Ah okej tack!
Calle_K skrev:Väntevärdet är en linjär operator, så det gäller att E[x+y] = E[x] + E[y] oavsett om x och y är oberoende eller inte.
Hur kom du föresten fram till att de är oberoende?
De är oberoende om rho=0.
Eller... egentligen så är det lite mer komplicerat, kolla i spoilern för detaljer.
Visa spoiler
De stokastiska variablerna är okorrelerade om rho=0. Okorrelerade variabler är inte nödvändigtvis oberoende, dock gäller det att oberoende variabler är okorrelerade.
För normalfördelade stokastiska variabler gäller det att om de är okorrelerade är de även oberoende, det finns alltså en ekvivalens mellan oberoende och okorrelerade.
Dock kräver vi enbart okorrelerade variabler för att säga att Var(X+Y)=Var(X)+Var(Y). Allmänt gäller det att Var(X+Y)=Var(X)+Var(Y)+2*Cov(X,Y) och om X och Y är okorrelerade gäller det att Cov(X,Y)=0.
I detta fall är Cov(X,Y)=rho*sigma1*sigma2=1/2. Därmed blir Var(X+Y)=Var(X)+Var(Y)+1
Ah okej då förstår jag tack!


