Beräkna P(|X + Y −3|< 0.01)

Hmmm, notera att $E(X)+E(Y)=1+2=3$. För oberoende normalfördelningar gäller det att: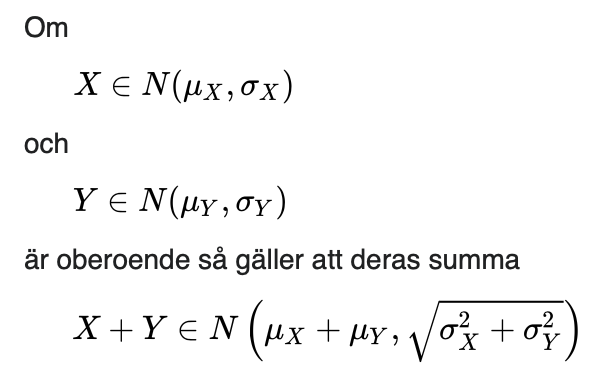

Det kanske kan gå att använda på något sätt? 

Yes, tack! Om någon annan behöver hjälp har ni min lösning här:

 $X+Y\in N(1+2, \sqrt{0,{01}^2+0,{01}^2}), dvs X+Y\in N(3, \sqrt{0,02})$

Sen skriver jag om lite 

$$\begin{gathered} P(\frac{2,99-3}{\sqrt{0,02}} < \frac{X+ Y -3}{\sqrt{0,02}} <\frac{3,01-3}{\sqrt{0,02}}) = \\ = P(-\frac{0,01}{\sqrt{0.02}} < \frac{X+ Y -3}{\sqrt{0,02}} < \frac{0,01}{\sqrt{0.02}}) \end{gathered}$$

Där $\frac{0,01}{\sqrt{0,02}}\approx 0,71$

Jag sätter nu $\frac{X+ Y -3}{\sqrt{0,02}} = Z \in N(0,1)$ och får:

$$\begin{gathered} P(Z<0,071)-P(Z<-0,071)=\phi (0,071)-\phi (-0,071)= \\ \phi (0,071)-(1-\phi (0,071\left)\right)=2\phi (0,071)-1 \end{gathered}$$

Om jag kollar i tabell får jag  $\phi (0,07)=0,5279$, vilket ger mig svaret $0,0558\approx 0,06$ som var rätt svar! :)

Det ser jättebra ut! Bara en liten detalj. Här:

Piggelinmatte skrev:

 

Jag sätter nu $\frac{X+ Y -3}{\sqrt{0,02}} = Z \in N(0,1)$ och får:

borde du, för att vara tydlig, skriva $\frac{X+ Y \mathbf{-}\mathit{E}\mathbf{\left(}\mathit{X}\mathbf{\right)}\mathbf{-}\mathit{E}\mathbf{\left(}\mathit{Y}\mathbf{\right)}}{\sqrt{0,02}} = Z \in N(0,1)$, så att (-3)-termen där inte blandas ihop med (-3)-termen i frågan. Om värdevärdena båda hade varit 2, skulle vi subtrahera fyra, inte tre. :)