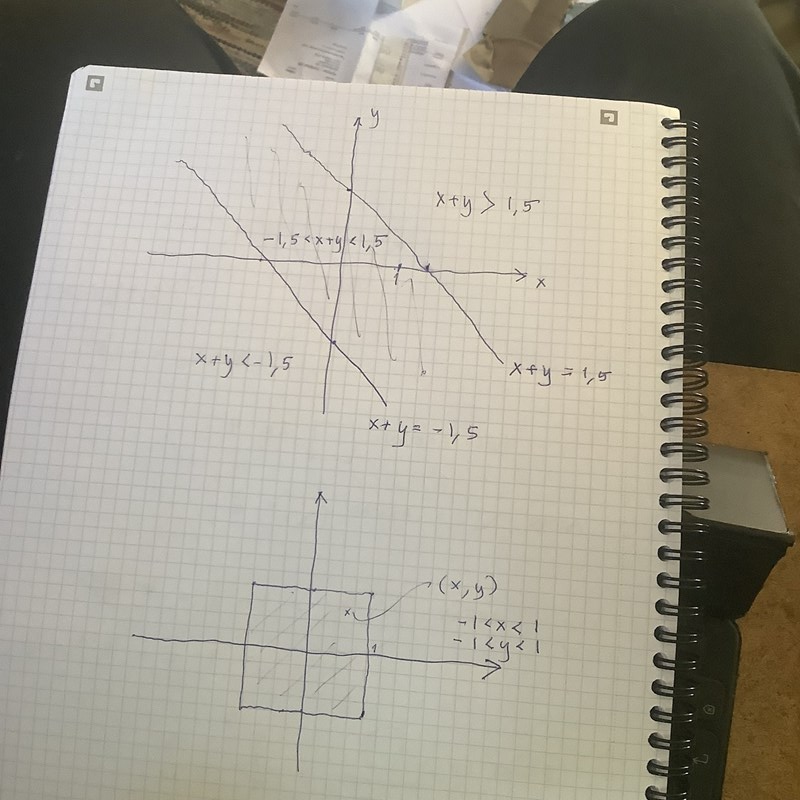
Beräkna P(-1,5<xi<1,5)
Hej! Jag försöker förstå vad jag gör för fel i denna uppgift? Jag får en sannolikhet större än 0:( När jag tittar i facit så har de gjort en liknande bild och det är arean A som ska vara sannolikheten, men jag måste göra något fel när jag beräknar dess area:(
Tack på förhand!
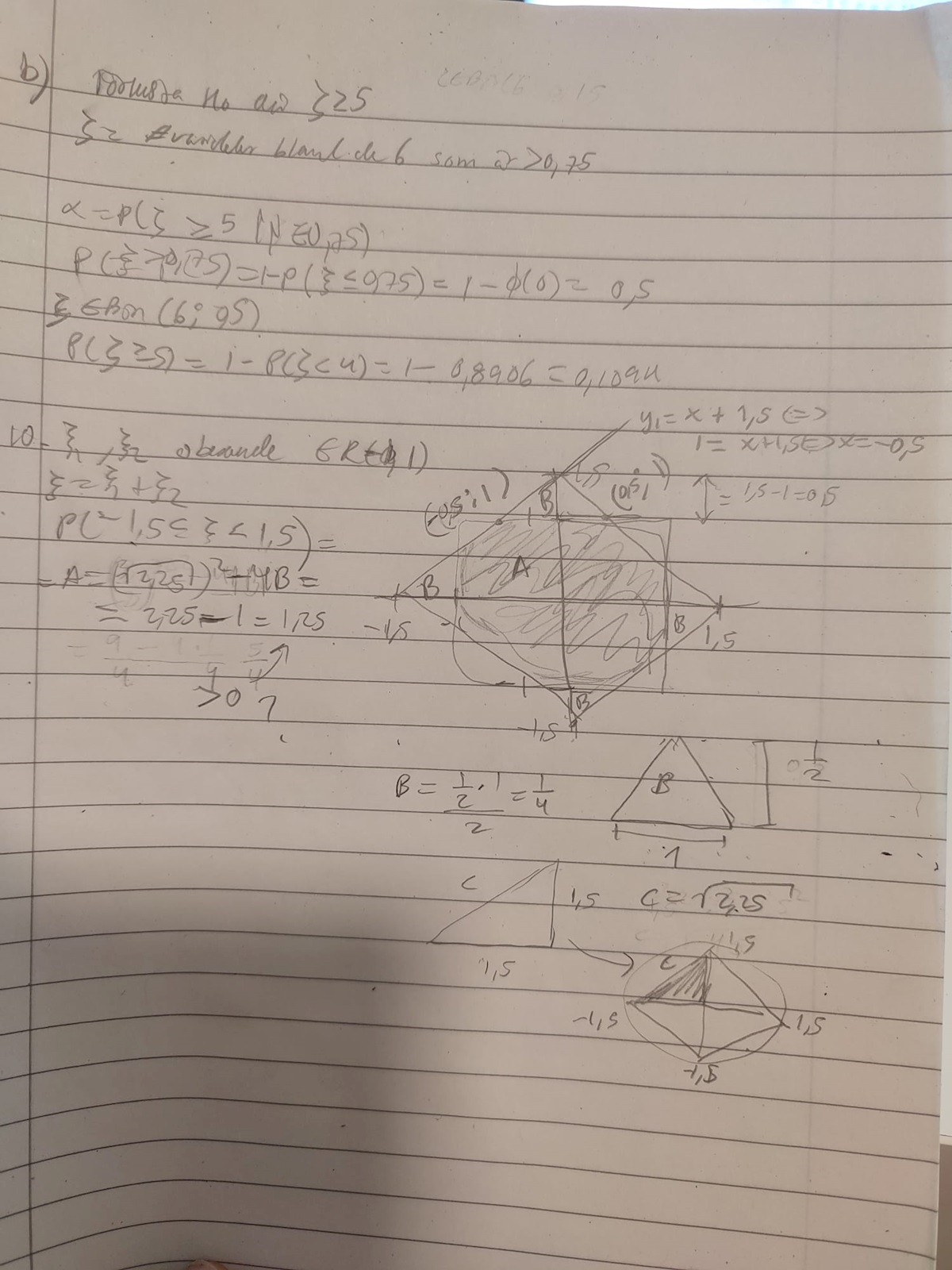
Mitt försök:

PS Det är litet lättare tycker jag att kalla xi-ett för x och xi-2 för y. Då ser man linjerna x+y = 1,5 och x+y = –1,5 klarare.
Marilyn skrev:PS Det är litet lättare tycker jag att kalla xi-ett för x och xi-2 för y. Då ser man linjerna x+y = 1,5 och x+y = –1,5 klarare.
Tack för svar och tack för tipset! Jag hade använt den andra fyrkanten för att beräkna totala arean men nu har jag använt samma som du och då även ändrat vilka trianglar jag subtraherar. Nu får jag samma ekvation som facit men de har skrivit ett annat svar konstigt nog:(
Min lösning:

Facit lösning:
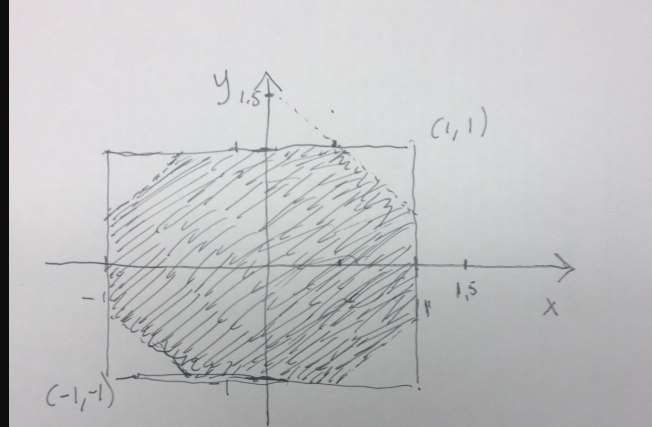

Facits svar: 0,9375
Så de har löst det på samma sätt som jag men svaret de använder är det du fått:) så vet inte riktigt vad som är rätt:(
Hmm, x+y = 1,5 är en rät linje. x+y > 1,5 är alla punkter ovanför linjen, x+y < 1,5 är punkterna under linjen. Så –1,5 < x+y < 1,5 är den gata som ligger mellan linjerna x+y = –1,5 och x+y = 1,5.
Men både x och y är mellan –1 och 1, så vi ska betrakta den del av kvadraten som ligger mellan de två linjerna. Men i din figur har du tagit bort hörnen uppe till vänster och nere till höger. Det blir fel. T ex i punkten (1, –1) är x+y = 0 och det ligger mellan minus och plus 1,5, eller hur?
Oj var det facits lösning där figuren var? Konstigt, då är jag inte med.
Villkoret –1,5 < x+y < 1,5 är en gata. Hur stor andel av kvadraten ligger på gatan?
Marilyn skrev:Oj var det facits lösning där figuren var? Konstigt, då är jag inte med.
Villkoret –1,5 < x+y < 1,5 är en gata. Hur stor andel av kvadraten ligger på gatan?
Hm jag vet inte jag har gjort den här uppgiften för 1-2 månader sedan så var nog så jag kom ihåg figuren och tänkte då att de tänker att både -1,5<xi1<1,5 och -1,5<xi2<1,5. Eller det är så jag hade uppfattat det och så jag tänkte nu. Dock verkar din lösning mycket mer tydlig och logisk så tror nog den stämmer bättre:)
”…då att de tänker att både -1,5<xi1<1,5 och -1,5<xi2<1,5.”
Hallå, om –1 < x < 1 och –1 < y < 1 så är det solklart att –1,5 < x < 1,5 och –1,5 < y < 1,5.
Marilyn skrev:”…då att de tänker att både -1,5<xi1<1,5 och -1,5<xi2<1,5.”
Hallå, om –1 < x < 1 och –1 < y < 1 så är det solklart att –1,5 < x < 1,5 och –1,5 < y < 1,5.
Det är sant!

Oj bilden blev på tvären, men skilj på ”gatan” och ”kvadraten”.
Marilyn skrev:
Oj bilden blev på tvären, men skilj på ”gatan” och ”kvadraten”.
Det är enkelt att rotera bilden - klicka på den!
Marilyn skrev:
Oj bilden blev på tvären, men skilj på ”gatan” och ”kvadraten”.
Tack det var en tydlig bild! Tror jag förstår bättre nu:)