Beräkna median, övre och undre kvartil för diskret slumpvariabel

Har fastnat på uppgift d) och undrar hur man ska motivera,
jag kom fram till att
Jag ritade upp fördelningsfunktionen och man kunde då inse vilket k värde respektive kvantil behövde anta för att uppnå kriterierna som nämns i uppgiften. Finns det något annat sätt att göra det på?
Kan du lägga in vad du kom fram till på fråga a) och c)?
Smaragdalena skrev:Kan du lägga in vad du kom fram till på fråga a) och c)?
Absolut,
Jag skulle rita upp utfallsrummet och ta fram var 25, 50 respektive 75% av arean hamnar. Jag vet ju att hela arean skall vara 1.
Tror inte det finns ngt bättre sätt på en sån liten uppgift. Handlar bara om att du ska förstå frågan egentligen.
Jag ritade upp utfallrummet men det hjälpte inte mig att lösa uppgiften då det inte finns någon som är lämplig att vara Q_1
Kan du lägga upp bilden här? Det borde inte vara särskilt svårt att räkna ut för vilket värde 50 % av alla utfall är på vardera sidan om ett lodrätt streck.
Du har fyra tänkbara utfall. Låt var och en av dem bli en rektangel med bredden 0,25 och höjden pn. Totala arean av de fyra rektanglarna är 1.
https://gyazo.com/d4d43e2d9a52ae48929040b4697e7355
gick inte att ladda up bild via forumet av någon anledning, vet inte om filen var för stor.
Men vi vet ju att för t.ex Q_1 så ska 25% av sannolikhetsmassan vara till vänster om Q_1 och 75% till höger, men K=1 har sannolikhet 0,63 och har 0% av sannolikhetsmassan till vänster och 0,37 till höger?
Minst 25% av massan ska vara till vänster(eller lika med Q1) och minst 75% av massan ska vara till höger(eller lika med Q1)
Om du kollar på olikheterna i uppgiften igen så har du likhet med, så den du är på får räknas till både höger och vänstersidan.
Om K=1 har sannolikheten 63 % så är både första kvartilen och medianen lika med 1. Det ser ut som om tredje kvaritlen har värdet 2.
Det verkar som om du behöver förstå vad median (och första och tredje kvartil betyder.
Tänk dig att vi bestämmer värdet på den stokastiska variabeln 99 gånger (ungefär hundra, mensådant att medianen och kvartilerna blir heltal). Då får vi ungefär 63 stycken ettor. Om vi ställer upp alla resultaten i storlekksordning kommer alltså både resultat nummer 25 (första kvadranten) och 49 (medianen) att ha värdet 1, och resultat nummer 74 (tredje kvartilen) blir 2. Om du hade gjort som jag skrev i mitt förra inlägg hade man kunnat beräkna areorna.
Det var inga problem att lägga in bilden: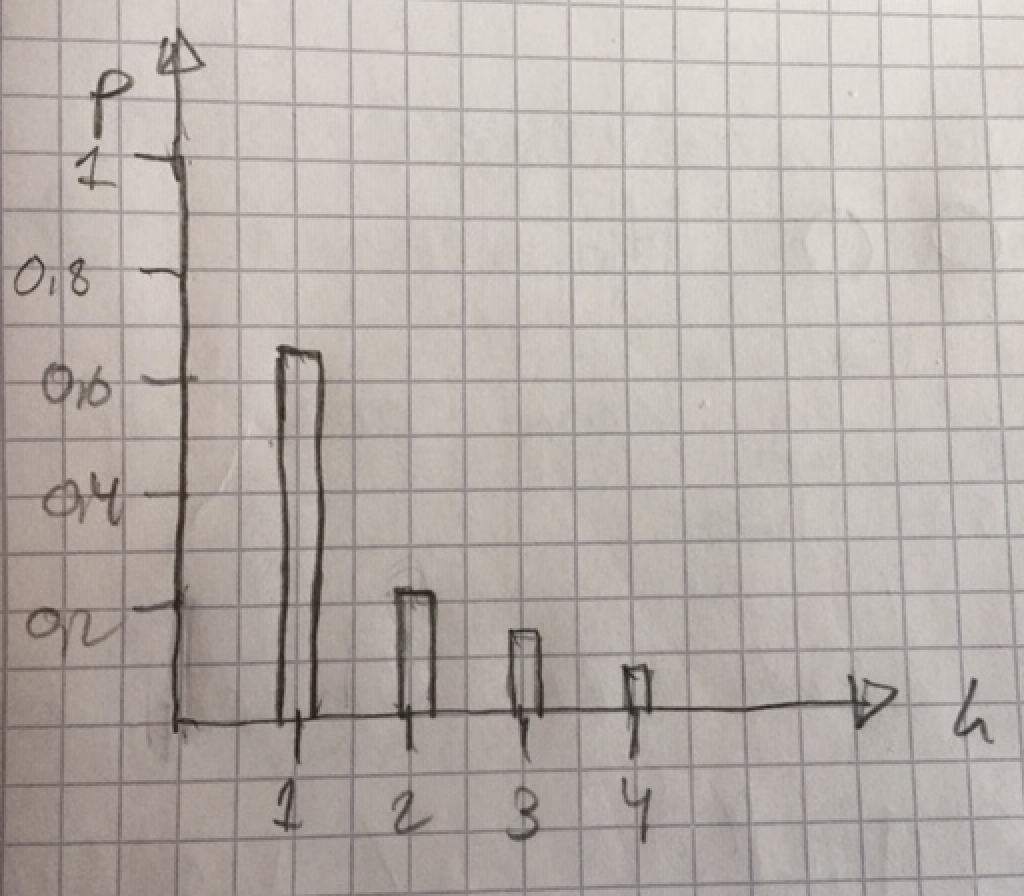
Jag fick också meddelande om att bilderna var för stora igår, fast jag gjorde som vanligt. Funkade igen efter en stund.
Smaragdalena skrev:Om K=1 har sannolikheten 63 % så är både första kvartilen och medianen lika med 1. Det ser ut som om tredje kvaritlen har värdet 2.
Det verkar som om du behöver förstå vad median (och första och tredje kvartil betyder.
Tänk dig att vi bestämmer värdet på den stokastiska variabeln 99 gånger (ungefär hundra, mensådant att medianen och kvartilerna blir heltal). Då får vi ungefär 63 stycken ettor. Om vi ställer upp alla resultaten i storlekksordning kommer alltså både resultat nummer 25 (första kvadranten) och 49 (medianen) att ha värdet 1, och resultat nummer 74 (tredje kvartilen) blir 2.
Super bra förklaring, tack så mycket för all hjälp! :)




