Beräkna längden av sträckan x

Förklaring av figuren:

• Den blåa sträckan r 20 cm.
• Den röda sträckan är 12 cm.
• Den gula sträckan är 6 cm 
• Den gula och den gröna sträckan är tillsammans x cm.
• De två markerade vinklarna är lika stora, vilket betyder att den blåa sidan är parallell med den röda sidan.

Kan man räkna ut den på detta vis x/6=12/20?

abcdefghijklmo skrev:

Kan man räkna ut den på detta vis x/6=12/20?

Pröva! Vad blir då x? Är det rimligt?

Nej, talet blev för lite. Skulle du kunna tipsa mig om annat?

Bra att du insåg att det inte var rimligt.

Tips: Eftersom den röda och den blåa sidan är parallella så är den röda sidan en parallelltransversal och då är den lilla övre triangeln likformig med den stora triangeln. Detta enligt topptriangelsatsen.

12/20=0,6

Vad ska göras sen?

Läs och använd det som står i detta avsnitt.

Fråga om det är något du inte förstår.

Okej så man kan dela upp den i två olika trianglar ADE och ABC. Men vi har ju inget värde på A så det blir lite klurigare..

Markera A, B, C, D och E i bilden och lägg upp den här.

Vad menar du med "värde på A"? Jag antar att du menar att A är ett hörn?

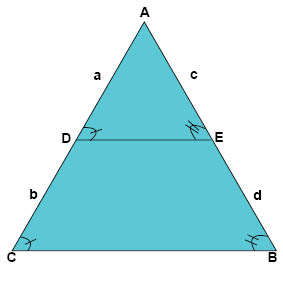
Tog denna från matteboken.se men menade på detta vis (om jag också skulle göra en triangel skulle den också se ut så)

OK. Är du med på att de båda trianglarna ABC och ADE är likformiga?

Är du med på att det betyder att $\frac{\bar{AD}}{\bar{AC}}=\frac{\bar{DE}}{\bar{BC}}$?

Där $\bar{AC}$ betyder längden av sträckan AC o.s.v.

Hur ska man börja räkna ut?

Svara på frågorna.

Ja, jag är med på det men jag blir lite förvirrad av vad A i det här fallet ska vara, kan man sätta det som hälften av x?

Nej, inte hälften.

Om du kallar längden av den gröna sträckan a (se bild) så gäller det att a + 6 = x.

Kommer du vidare då?

a+6=12/20

Är väldigt osäker och skulle gärna vilja ha en förklaring på hur man löser uppgiften

Är du med på att likformigheten ger att a/x = 12/20?

På vilket sätt blir det så, kan du förklara?

Det är precis samma sak som det jag skrev i svar #12 (och som du sa att du var med på):

Förhållandet mellan den lilla triangelns vänstra sidlängd ($\bar{AD}$) och den stora triangelns vänstra sidlängd ($\bar{AC}$) är lika med förhållandet mellan den lilla triangelns undre sidlängd ($\bar{DE}$) och den stora triangelns undre sidlängd ($\bar{BC}$). Alltså $\frac{\bar{AD}}{\bar{AC}}=\frac{\bar{DE}}{\bar{BC}}$.

I uppgiftens triangel är den lilla triangelns vänstra sidlängd $a$, den stora triangelns vänstra sidlängd $x$, den lilla triangelns undre sidlängd $12$ och den stora triangelns undre sidlängd $20$. Alltså $\frac{a}{x}=\frac{12}{20}$.

======

Allt detta pga att i båda fallen är den lilla och den stora triangeln likformiga, vilket innebär att förhållandet mellan respektive sidlängder är lika stort.

Läs gärna mer om likformighet och vad det innebär här.