Beräkna kroppens volym uppgift 8.2

Har du kommit fram till hur området ser ut?

Lasse Vegas skrev:

Har du kommit fram till hur området ser ut?

Ja mha desmos ser det väl ut såhär:

Blåa området du har ritat stämmer inte helt, det ska inte vara paranteser omkring x^2-y^2.

Lasse Vegas skrev:

Blåa området du har ritat stämmer inte helt, det ska inte vara paranteser omkring x^2-y^2.

Aa ok. Nu blir det såhär:

Yeah det där ser bättre ut. Vad du skulle kunna göra är att kolla på området ovaninfrån. Hur ser det ut då?

Lasse Vegas skrev:

Yeah det där ser bättre ut. Vad du skulle kunna göra är att kolla på området ovaninfrån. Hur ser det ut då?

Är ej säker på vad du menar med att kolla på området ovanifrån. Jag vet ej hur man gör det manuellt. Något sånt kanske?

Tänk att positiva z-axeln är riktad uppåt, då om man kollar ner på området får man en yta i 2d som kan hjälpa i det här fallet.

Lasse Vegas skrev:

Tänk att positiva z-axeln är riktad uppåt, då om man kollar ner på området får man en yta i 2d som kan hjälpa i det här fallet.

Den blåa är en yta ja. Jag har dessa gränser justnu.  Jag använder mig av cylindriska koordinater

Aa cylindriska koordinater är bra i det här fallet. Vad jag menar tidigare är att man ser att skärningen mellan ytorna ger en cirkel i xy-planet. På det sättet får man en yta som man sedan integrerar över.

Lasse Vegas skrev:

Aa cylindriska koordinater är bra i det här fallet. Vad jag menar tidigare är att man ser att skärningen mellan ytorna ger en cirkel i xy-planet. På det sättet får man en yta som man sedan integrerar över.

Okej men jag är fortfarande fast. Jag satte som sagt ytorna med varandra och fick z=1

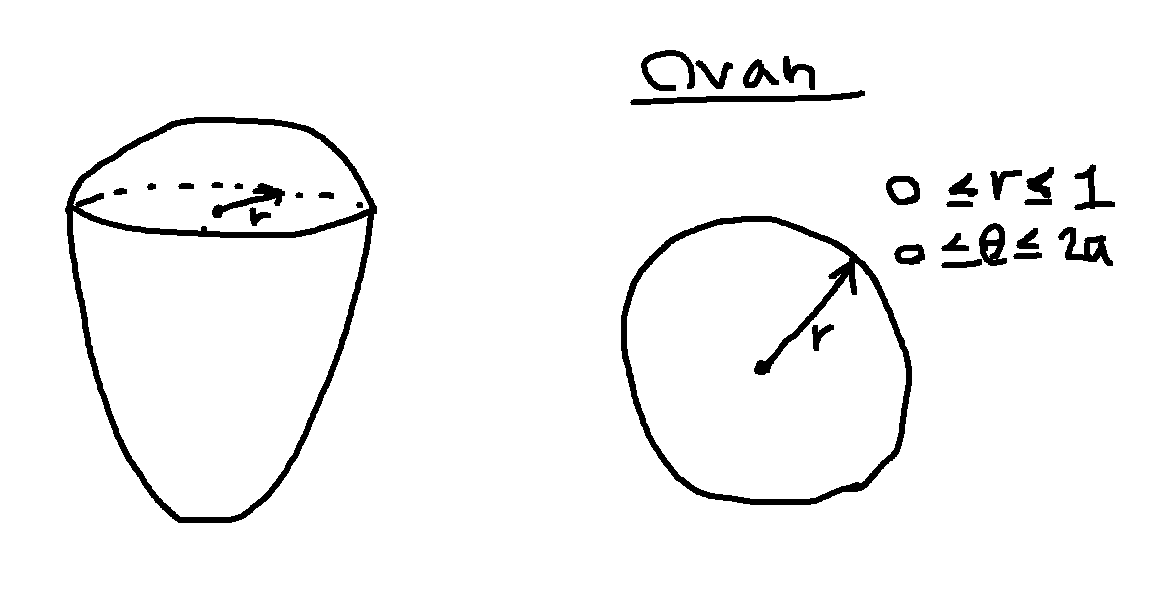Till vänster har vi en halvbra skiss av området och till höger har vi hur området ser ut ovaninfrån. Vi ser att det blir en skiva och då blir det lätt att få fram gränserna för r och theta.

Lasse Vegas skrev:

Till vänster har vi en halvbra skiss av området och till höger har vi hur området ser ut ovaninfrån. Vi ser att det blir en skiva och då blir det lätt att få fram gränserna för r och theta.

Ja gränserna är ju de du skrev upp och jag påbörjade integreringen redan.

Jag har sagt att vi kollar ovanfrån men mer matematiskt sagt är väl att man projicerar området på xy-planet så att det blir platt.

Lasse Vegas skrev:

Jag har sagt att vi kollar ovanfrån men mer matematiskt sagt är väl att man projicerar området på xy-planet så att det blir platt.

Ja jag fortsätter med integreringen i #9

destiny99 skrev:

Lasse Vegas skrev:

Till vänster har vi en halvbra skiss av området och till höger har vi hur området ser ut ovaninfrån. Vi ser att det blir en skiva och då blir det lätt att få fram gränserna för r och theta.

Ja gränserna är ju de du skrev upp och jag påbörjade integreringen redan.

Lite svårt att se vad som står i uttrycket. Jag tror att du kan ha missat att lägga till r bland diffirentialerna när du skrev om till cylindriska koordinater.

Edit: Råkade citera fel. Jag syftar på beräkningen du skickade.

Det borde bli att du byter ut dx*dy mot r*dr*dθ. Annars ser uttrycket rätt ut.

Jag ser inte z^2 i högra ekvationen

Du har fel kropp där och därmed fel gränser.

Trinity2 skrev:

Jag ser inte z^2 i högra ekvationen

Du har fel kropp där och därmed fel gränser.

Jag tror att vi håller på med uppgift 8.2 för tillfället.

Mitt fel! Mi scusi!

Blev lite fundersam och var tvungen att kolla några extra gånger haha. Var ju faktiskt nästan likadana ekvationer i båda uppgifterna.

Lasse Vegas skrev:

Blev lite fundersam och var tvungen att kolla några extra gånger haha. Var ju faktiskt nästan likadana ekvationer i båda uppgifterna.

Hörni här är mitt svar. Men facit svarar såhär : 

Det kan vara så att ni har svarat på olika former. T.ex så har de faktoriserat ut pi/6 i facit. Prova att förenkla ditt svar genom att faktorisera ut saker som går, sen kan du försöka bli av med exponenten vid 2:an.