Beräkna krafterna i linorna
Hej!
Jag kommer ej vidare på den här uppgiften. Jag tänker att jag ska ställa upp en jämviktsekvation och en momentekvation, men lyckas ej komma fram till exakt var plåtens masscentrum ligger. Jag har kommit fram till att den är i den högra biten (uppenbarligen) samt att den högra biten väger 3ggr så mycket som den vänstra halvan. Hur ska jag komma vidare? Finns det något smidigare sätt?


Det borde stå i formelsamlingen, men tyngdpunkten ligger på x = 4a/3 om vänstra hörnet är origo.
Tack! Det gjorde det inte, men hittade en gammal där det stod.
Jag har räknat uppgiften nu men får inte helt rätt. Jag har tagit fram jämviktsekvationen i vertikalled, momentekvationen kring kraft N1 samt ett deformationsvillkor. Jag räknar på mycket små deformationer, så δ<<l, där l är repets ursprungslängd.
Jag har skrivit rätt svar längst ner. Är deformationsvillkoret jag har satt upp felaktigt?

Jag har inte kollat dina uträkningar, men eftersom mittlinan är precis i mitten, och linorna förlängs i en rät linje (överkanten på triangeln) så måste förlängningen för mittlinan ligga mitt emellan förlängningarna för de andra, och då gäller samma för krafterna.
Ditt svar 4/15 ligger inte mitt emellan 1/5 och 8/15.
Du har ett felaktigt deformationsvillkor. Du tvingar i nuvarande försök δ1 till noll som om du bara har en led vänstra punkten som plåten kan rotera kring. Därför får du inte rätt linkrafter.
Låt även deformation ske för första linan i din figur så löser du säkert problemet.
Angående tyngdpunkt
Kom ihåg att du kan räkna ut avstånd till tyngdpunkt ganska lätt med integraler, läs mer här:
https://engineeringstatics.org/centroids-by-integration.html
Sedan har du väl annars Physics Handbook eller liknande, hoppas jag? Där finns tyngdpunkt för alla standardgeometrier.
Tack för all hjälp! Det löste sig när jag fick rätt på deformationsvillkoret!
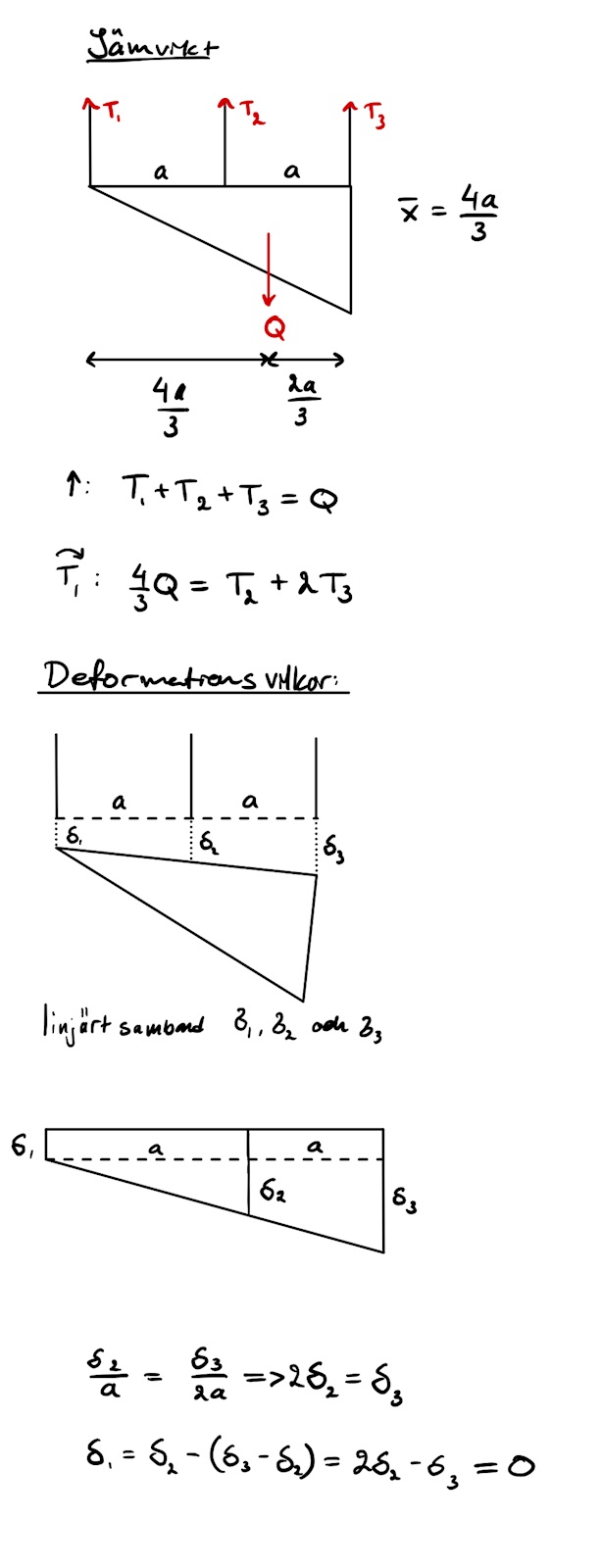
Jag har fastnat på samma uppgift och lyckas inte formulera deformationsvillkoret korrekt. Hur är förlängningen av vänstra snöret (delta 1) beroende av de andra? Det är linjärt men mitt försök till att utrycka det i delta 2 eller 3 resulterar till att delta 1 = 0. där delta 1 ska var m i Y = kx + m, har jag några randvillkor jag missar? Vad gör jag fel?
Se vad Laguna skriver i #4. δ2=δ1+δ32.
Tack så mycket! Det flög mig över huvudet :)




