Beräkna kongruensekvationssystem utan Kinesiska restsatsen?
Hej!
Har följande uppgift med tillhörande facit:

facit:
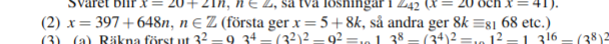
Observera att Kinesiska restsatsen uttryckligen inte ingår i min kurs och jag inte får använda den :(
Min lösning:

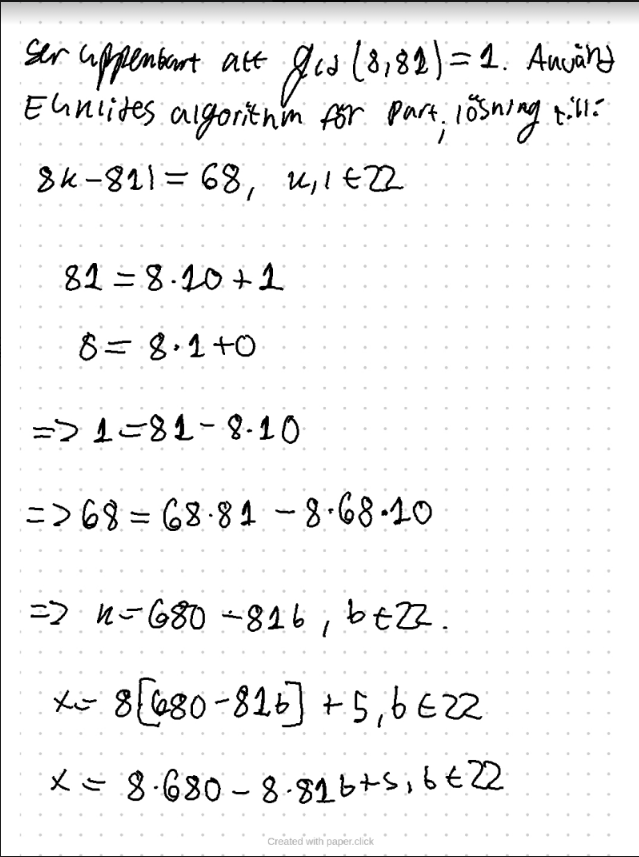

Kan väl förtydliga att det jag gör här
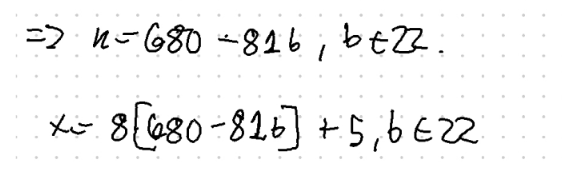
är att jag infogar i .
Jag har alltså lite problem med 5445.
En AI-kamrat online säger detta

men det är ju fel, .
Teckenfel. K=-680 om du kollar noga
Micimacko skrev:Teckenfel. K=-680 om du kollar noga
Ah, ok!
Men jag får ändå inte rätt svar.
Att
ger att
Så mina följdfrågor blir:
Hur får man fram 397 som facit gör?
Och om det stämmer att det är så här man ska göra, dvs. reducera modulo 648 enligt screenshoten från "En AI-kamrat online säger detta", då undrar jag:
Vad menas med att "lösningen är periodisk med 648", eller snarare det jag inte förstår där är varför det är legit att reducera 5435 modulo 648.
Varför - 81b? Du skrev i början att x=8k+5, håll dig till det. Ingen aning om vad AI gör, men de brukar inte vara så bra på att räkna.
Micimacko skrev:Varför - 81b? Du skrev i början att x=8k+5, håll dig till det. Ingen aning om vad AI gör, men de brukar inte vara så bra på att räkna.
Nej det har jag märkt att de är ganska dåliga på:)
Kika på denna del av min lösning, sorry om det är lite otydligt!
 Jag vill lösa , eftersom jag vill hitta i Z81. Jag får partiulärlösningen och eftersom 680, 81 är relativt prima ges alla lösningar till av där b är något heltal.
Jag vill lösa , eftersom jag vill hitta i Z81. Jag får partiulärlösningen och eftersom 680, 81 är relativt prima ges alla lösningar till av där b är något heltal.
Sen infogar jag detta i det faktum att .
Nämnvärt att denna del av lösningen (att x=konstant+648b), stämmer överrens med facit. Det är bara ”konstant” som jag får fel på.
Blir det lite klarare nu hur jag tänker?
Jag tror jag kom på vad som blev fel. Jag får rätt svar tekniskt sett:


